DataStructure

数据结构

时间复杂度（时间复杂度及空间复杂度）

摩尔定律（每18个月运行内存都会更新，空间复杂度不再特变关注）

• 用常数1取代运行时间中所有加法常数
• 在修改后的运行次数函数中，只保留最高阶项
• 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶

//计算时间复杂度
//1.
x=0;
for(i=1;i<=n;i++)
    for(j=1;j<=n-i;j++)  //i=1时内循环执行n-1次;i=2时执行n-2次...;i=n-1时执行1次
        x++;
//因为x++共执行了n-1+n-2+...+1=n(n-1)/2,所以执行时间为O(n^2)
//2.
i=1;
while(i<=n)
    i=i*3;
//O(log3^n)
//3.
void Func4(int N)
{
    int count=0;
    for(int k=00;k<100;++k)
    {
        ++count;
    }
    printf("%d\n",count);
}
//O(1)时间复杂度是只能运行常数次，不代表算法运行一次
//4.计算strchar的时间复杂度
const char * strchr(const char * str ,int character)
//strchar指的是在字符串中查找一个字符
/*
hellow world
假设查找的是h  最好情况:任意输入规模最小运行次数
假设查找的是w  平均情况:任意输入规模期望运行次数
假设查找的是d  最坏情况:任意输入规模最大运行次数
*/
while(*str)
{
    if(*str==character)
        return str;
    else
        ++str;
}
//O(N)
//当一个算法随着输入不同，时间复杂度不同，时间复杂度做悲观预期，看最坏情况

//计算冒泡排序的时间复杂度 同上1.
void BubbleSort(int* a,int n)
{
    assert(a);
    for(size_t end=n;end>0;--end)
    {
        int exchange=0;
        for(size_t i=1;i<end;++i)
        {
            if(a[i-1]>a[i])
            {
                Swap(&a[i-1],&a[i]);
                exchange=1;
            }
            if(exchange==0)
                break;
        }
    }
}
//n-1+n-2+...+1=n*(n-1)/2则时间复杂度为O(n^2)
//看算法复杂度不能只看是几层循环

int BnarySearch(int* a,int n,int x)
{
    assert(a);
    int begin=0;
    int end=n;
    while(begin<end)
    {
        int mid=begin+((end-begin)>>1);
        if(a[mid]<x)
            begin=mid+1;
        else if(a[mid]>x)
            end=mid;
        else
            return mid;
    }
    return -1;
}
//时间复杂度为log2^N;
//最好情况O(1);
//最坏情况O(log2^N);找不到的情况
/*
假设找了x次，元素一共有N个
1*2*2*2……=N
*/

//斐波那契算法的时间复杂度
long long Fib(size_t N)
{
    if(N<3)
        return 1;
    return Fib(N-1)+Fib(N-2);
}
//递归算法时间复杂度:递归次数*每次递归调用的次数，在这里每次递归调用的次数为常数1

消失的数字

//数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数，要求时间复杂度在O(n)内
/*
先给一个值x=0
x先跟[0,n]的所有值异或
x再跟数组中每个值异或
最后x就是缺的那个数字
*/
/*
异或:(先转化为2进制数)相同返回0，不同返回1,0和任何数字异或都为其本身,两个相同的数异或为0;异或满足交换律和结合律
*/
int missingNumber(int* nums,intt numsSize)
{
    int x=0;
    //跟[0,n]异或
    for(int i=0;i<=numsSize;++i)//注意这里是<=
    {
        x^=i;
    }
    //再跟数组中值异或
    for(int i=0;i<numsSize;++i)
    {
        x^=num[i];
    }
    return x;
}

//异或问题的拓展
//找出一个数组中出现一次的数(其它数出现了2次)
int[]arr={1,2,3,4,5,6,7,6,5,4,3,2,1};
int x=0;
for(int i=0;i<arr.length;i++)
{
    x=x^arr[i];
}
//找出数组当中出现两次的数
int []arr={1,2,3,4,5,6,7,3};//x^x^y=y
//(A^B^C^B)^(A^B^C)=(A^C)^(A^B^C)=B
int x=0;
for(int i=0;i<arr.length;i++)
{
    x=x^arr[i];
}
for(int i=1;i<=7;i++)
{
    x=x^i;
}
return x;

旋转数组

//给定一个数组，将数组中的元素向右移动k个位置，其中k是非负数  O(1)  相当于是旋转k次
/*
旋转数组的方法:
输入:nums=[1,2,3,4,5,6,7],k=3
输出:[5,6,7,1,2,3,4]
解释:
向右旋转1步:[7,1,2,3,4,5,6]
向右旋转2步:[6,7,1,2,3,4,5]
向右旋转3步:[5,6,7,1,2,3,4]
*/

/*
输入:num=[1,2,3,4,5,6,7],k=3
输出:num=[5,6,7,1,2,3,4]
方法:
( 4 3 2 1 ) 5 6 7   前n-k个逆置
4 3 2 1 ( 7 6 5 )   再后k个逆置
( 5 6 7 1 2 3 4 )   整体逆置
时间复杂度O(N) 空间复杂度O(1)
*/
void Reverse(int* nums,int left,int right)//逆置算法
{
    while(left<right)
    {
        int temp=num[left];
        num[left]=num[right];
        num[right]=temp;
        ++left;
        --right;
    }
}
void rotate(int* num,int numsSize,int k)
{
    if(k>=numsSize)
        k%=numsSize;
    //前n-k个数逆置
    Reverse(nums,0,numsSize-k-1);
    //后k个逆置
    Reverse(num,numsSize-k,numsSize-1);
    //整体逆置
    Reverse(nums,0,numsSize-1);
}
/*
当k==n时，相当于不旋转
当k>n时，相当于旋转k%n次
*/

顺序表

本质就是数组，但是存储的数据不能跳跃要连续

缺陷：

1.空间不够了需要增容，需要付出代价

2.为避免频繁扩容，我们基本都是扩2倍，空间浪费

3.顺序表要求数据从开始位置连续存储，那么我们在头部或者中间位置插入删除数据就需要挪动数据

realloc扩容有两种方式

• 原地扩容，后面如果有足够大的内存空间，返回原空间地址，代价小
• 异地扩容 ，如果后面没有足够大的内存空间，会找一块足够大的空间，将原空间内容拷贝过来并释放原空间，返回的是新空间地址，代价大

//SeqList.h
#prama once
#define N 100
typedef SLDataTpye;
//动态顺序表
typedef struct SeqList
{
    SLDataType* a;
    int size;//表示数组中存储了多少个数据
    int capasity;//数组实际能存储数据的空间容量是多大
}SL;
//接口函数--命名风格是跟着STL走的
void SeqListInit(SL* ps);//初始化
void SeqListPushBack(SL* ps,SLDataType x);
void SeqListPopBack(SL* ps);
void SeqListPushFront(SL* ps,SLDataType x);//前插
void SeqListCheckCapacity(SL* ps);//检查是否需要增容
void SeqListPopFront(SL* ps);

//SeqList.c
//顺序表初始化相当于尾插
void SeqListInit(SL* ps)
{
    ps.a=NULL;
    ps.size=ps.capacity=0;
}
//检查是否需要增容
void SeqListCheckCapacity(SL* ps);
{
     //如果没有空间或者空间不足，那么我们就扩容
    if(ps->size==ps->capasity)
    {
        int capasity=ps->capasity==0? 4:ps->capasity;
        SLDataType* tmp=(SLDataType*)realloc(ps->a,newcapacity*sizeof(SLDataType));
        if(tmp==NULL) //如果没有扩容成功，直接退出
        {
            printf("realloc fail\n")
                exit(-1);
        }
        ps->a=tmp;
        ps->capacity=newcapacity;
    }
}

void SeqListPushBack(SL* ps,SLDataType x)
{
    SeqListCheckCapacity(ps);//检查增容
    ps->a[ps->size]=x;
    ps->size++;
}

void SeqListPushBack(SL* ps,SLDataType x);
void SeqListPopBack(SL* ps);
void SeqListPushFront(SL* ps,SLDataType x);
void SeqListPopFront(SL* ps);

#include "SeqList.h"
void SeqListInit()
{
    SL s1;
    SeqListInit(s1);
}
int main()
{
    //TestSeqList1();
    TestSeqList2();
    return 0;
}

//Text1.c
#include "SeqList.h"
void TestSeqList1()
{
    SL s1;
    SeqListInit(&s1);
    SeqListPushBack(&s1,1);
    SeqListPushBack(&s1,2);
    SeqListPushBack(&s1,3);
    SeqListPushBack(&s1,4);
    SeqListPrint(&s1);
}

//头插法(把一个数据x插入最前面)
void SeqListPushFront(SL* ps,SLDataType x)
{
    //当释放数据时会检查数据是否越界，越界就会报错，如果满了就需要增容
    
    SeqListCheckCapacity(ps);//考虑是否需要增容
    
    //挪动数据
    int end=ps->size-1;//end开始指向最后数据的下标值
    while(endl>=0)
    {
        ps->a[end+1]=ps->a[end];
        --end;
    }
    ps->a[0]=x;
    ps->size++;
}
//Text2.c
void TestSeqList2()
{
    SL s1;
    SeqListInit(&s1);
    SeqListPushBack(&s1,1);
    SeqListPushBack(&s1,2);
    SeqListPushBack(&s1,3);
    SeqListPushBack(&s1,4);
    SeqListPrint(&s1);
    
    SeqListPushFront(&s1,10);
    SeqListPushFront(&s1,20);
    SeqListPushFront(&s1,30);
    SeqListPrint(&s1);
    SeqListPopFont(&s1);
}



//头删(因为顺序表要求从头开始存储，并且连续，所以size--是尾删)从前向后覆盖
void SeqListPopFont(SL*)//
{
    assert(ps->size>0);//(暴力方式)判断顺序表中有没有数据
    //挪动数据
    
    int begin=1;//使begin为下标1，也就是第二个数据的下标
    while(begin<size)
    {
        ps->a[begin-1]=ps->a[begin];
        ++begin;
    }
}


//查找一个值x的位置，找到返回x位置下标，没有返回-1
int SeqListFind(SL* ps,SLDataType x)
{
    for(int i=0;i<ps->size;i++)
    {
        if(ps->a[i]==x)
        {
            return i;
        }
    }
    return -1;//暴力求解
}


//在pos位置前插入数据
void SeqListInsert(SL* ps,int pos,SLDataType x);
{
    /*1.
    if(pos>ps->size||pose<0)//pos可以等于size，选择尾插
    {
        printf("pos invalid\n");
        return;
    }
    */
    //2.
    assert(pos>=0&&pos<=ps->size)//括号为假就报错
        SeqListCheckCapacity(ps);//考虑是否需要增容
    int end=ps->size-1;
    while(end>=pos)
    {
        ps->a[end+1]=ps->a[end];
        end--;
    }
    ps->a[pos]=x;
    ps->size++;
}


//删除pos位置的数据
void SeqListEarse(SL* ps,int pos); 
{
    assert(pos>=0 && pos<ps->size);
    int begin=pos+1;//使begin指向要删除位置数据的后一位
    while(begin<ps->size)
    {
        ps->a[begin-1]=ps->a[begin];
        ++begin;
    }
    ps->size--;
}

链表

//SList.c
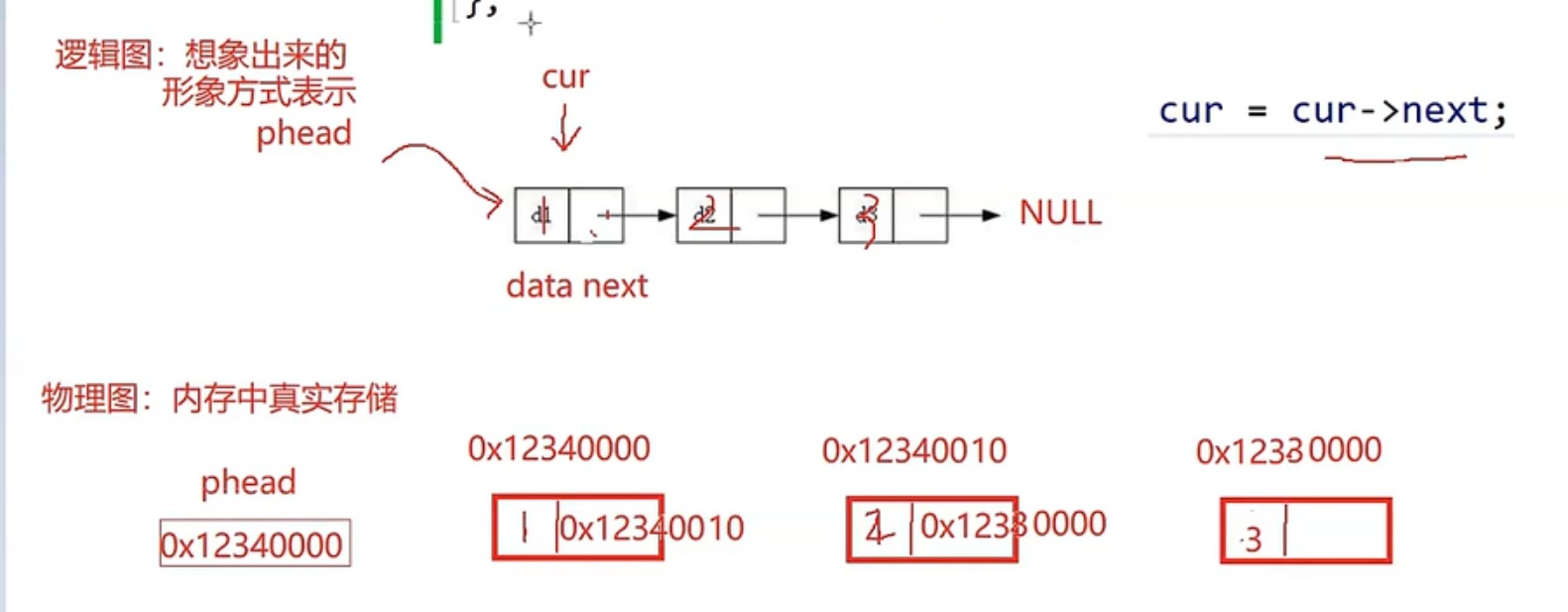
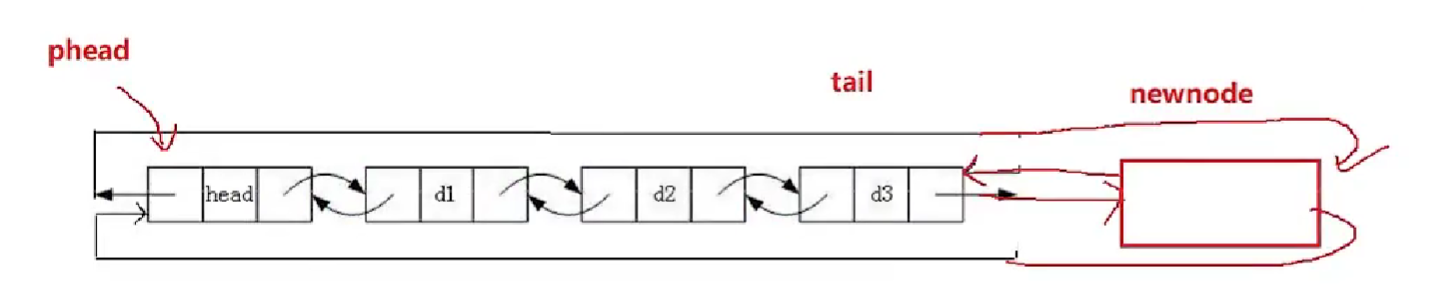
void SListPrint(SLTNode* phead)
{
    SLTNode* cur=phead;//cur是一个指向结构体的指针
    while(cur!=NULL)
    {
        printf("%d->",cur->data);
        cur=cur->next;//地址指针不连续
    }
}
//void SListPushBack(SLTNode* phead,SLTDateType x)

//1.尾插，为了解决插入第一个节点的问题要用二级指针，第二个就不用了，因为第二个改变的是结构体
void SListPushBack(SLTNode** pphead,SLTDateType x)
{
    SLTNode* newnode=(SLTNode*)malloc(sizeof(SLNode));
    newnode->data=x;
    newnode->next=NULL;
    
    if(*pphead==NULL)
    {
        *pphead=newnode;
    }
    else
    {
        //找到尾节点
    SLTNode* tail=*pphead;
      while(tail->next!=NULL)
      {
          tail=tail->next;
      }
        
    tail->next=newnode;
    }
   
}


//2.头插
void SListPushFront(SLTNode** pphead,SLTDateType x)
{
   SLTNode* newnode=BuyListNode(x);
    /*
    SLDNode* BuyListNode(SLTDateType x)
    {
    SLTNode*newnode=(SLTNode*)malloc(sizeof(SLTNode));
    if(newnode==NULL)
    {
      printf("malloc fail\n");
      exit(-1);
    }
    newnode->data=x;
    newnode->next=NULL;
    return newnode;
    }
    
    */
    newnode->next=*pphead;
    *pphead=newnode;
}


//3.尾删,如果删完就需要二级指针
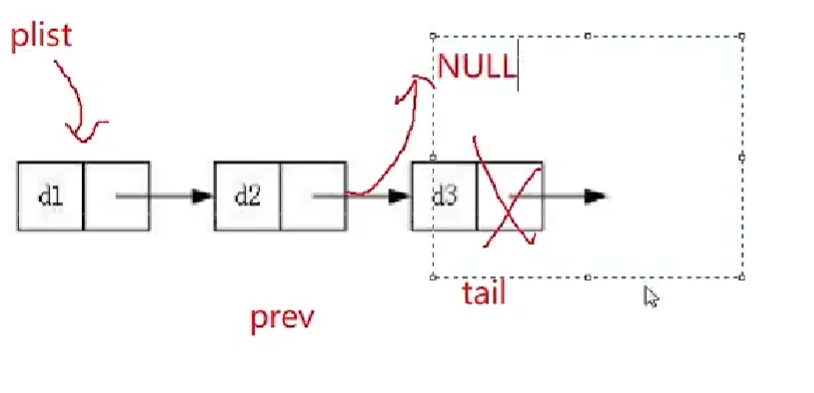
void SListPopBack(SLTNode**pphead)
{
    if(*pphead==NULL)
    {
        return;
    }
    
    if((*pphead)->next==NULL)//只有一个节点
    {
        free(*pphead);
        *pphead=NULL;
    }
    else
    {
        SLTNode* prev=NULL;
        SLTNode* tail=*pphead;
        while(tail->next!=NULL)
      {
        prev=tail;
        tail=tail->next;
      }
        free(tail);
        tail=NULL;//打印的时候要预防野指针问题，所以加下一行代码
        prev->next=NULL;
    }
}


//4.头删
void SListPopFront(SLTNode** pphead)
{
    if(*pphead==NULL)
        return;
    SLTNode* next=(*pphead)->next;
    free(*pphead);
    *pphezd=next;
}

//5.查找
SLTNode* SListFind(SLTNode* phead,SLTDateType x)
{
    SLTNode* cur=phead;
    while(cur)
    {
        if(cur->data==x)
        {
            return cur;
        }
        else
        {
            cur=cur->next;
        }
    }
    return NULL;
}

//6.在pos前插入一个节点
SLTNode* SListInsert(SLTNode* phead,STNode* pos,SLTDateType x)
{
    SLTNode* newnode=BuyListNode(x);
    newnode->next=pos->next;
    pos->next=newnode;
}

//7.删除pos节点
void SListEraes(SLTNode** pphead,SLTNode* pos)
{
    //特殊情况要删除头节点
    if(*pphead==pos)
    {
        *pphead=pos->next;
        free(pos);
    }
    else
    {
        SListNode* prev=*pphead;
        while(prev->next!=pos)
        {
            prev=prev->next;
        }
        prev->next=pos->next;
        free(pos)
    }
}

prev图如上

//SLisst.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
typedef int SLDataType
    
typedef struct SListNode
{
    SLDataType data;//定义一个数据类型为SLDataType的数据
    struct SListNode* next;//节点(结构体)指针指向下一个节点，存的是下一个节点的地址
}SLTNode;

void SListPrint(SLTNode* phead);//不会改变phead的值不用传二级
void SListPushBack(SLTNode** pphead,SLTDateType x);//尾插一个新节点1.找到原来的尾(尾的标志是该节点所存的地址是空)2.让原来最后节点指向要插入的节点

void SListPushFront(SLTNode** pphead,SLTDateType x);

//查找
SLTNode* SListFind(SLTNode* phead,SLTDataType x);

//Test.c
#include"SList.h"
void TestSList1()
{
   // SListNode* plist=NULL;phezd和plist都是指向首节点的指针  问题是形参phead的改变没有影响实参plist
    SListNode* plist=NULL;
    SListPushBack(&plist,1);
    SListPushBack(&plist,2);
    SListPushBack(&plist,3);
    SListPushBack(&plist,4);
    SListPrint(plist);
    
    SListPushFront(&plist,1);
    SListPushFront(&plist,2);
    SListPushFront(&plist,3);
    SListPushFront(&plist,4);
}

void TestSList2()
{
    SListPushFront(&plist,1);
    SListPushFront(&plist,2);
    SListPushFront(&plist,3);
    SListPushFront(&plist,4);
    SListPopBack(&plist);
    
    SListPrint(plist);
}

void TestSList3()
{
    SListPushFront(&plist,1);
    SListPushFront(&plist,2);
    SListPushFront(&plist,3);
    SListPushFront(&plist,2);
    SListPushFront(&plist,4);
    SListPushFront(&plist,2);
    
    SLTNode* pos=SListFind(plist,2);
    int i=1;
    while(pos)//当要寻找的值在链表中出现好几次时
    {
        printf("第%d个pos节点:%p->%d\n",i++,pos,pos->data);
        pos=SListFind(pos->next,2)
    }
    //修改3->30
    pos=SListFind(plist,3)
        if(pos)
        {
            pos->data=30;
        }
    SListPrint(plist);
}

int main()
{
    return 0;
    TestSList1();
    TestSList2();
}

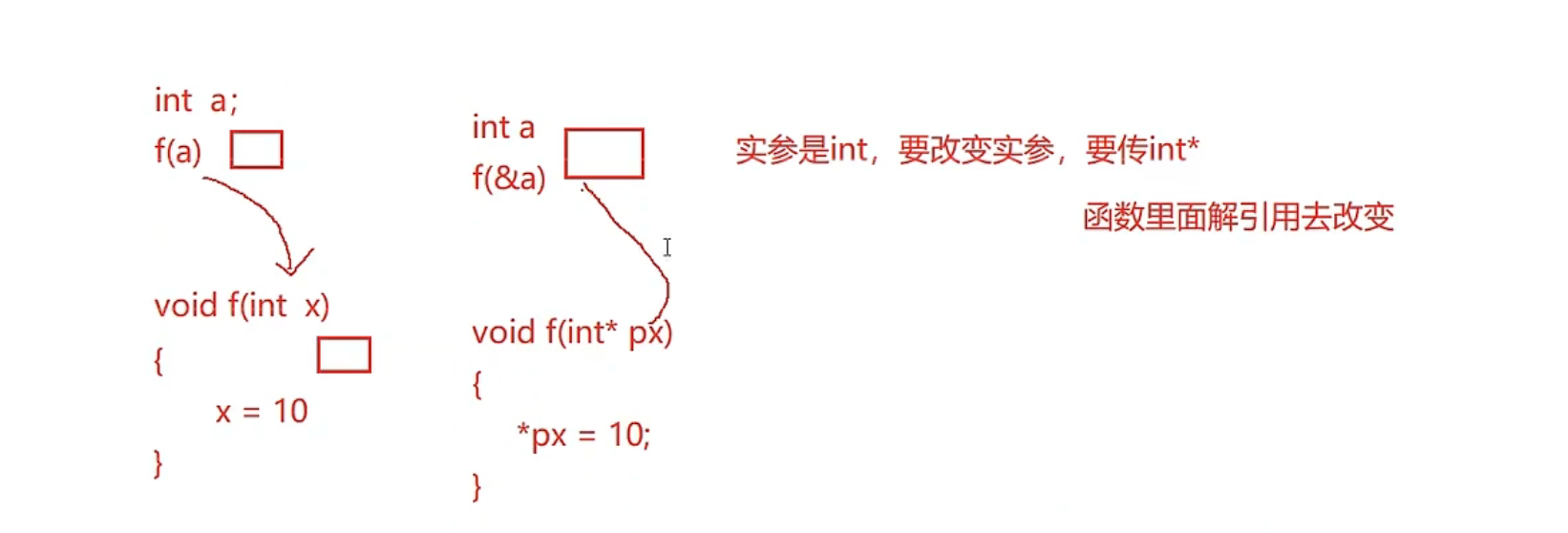
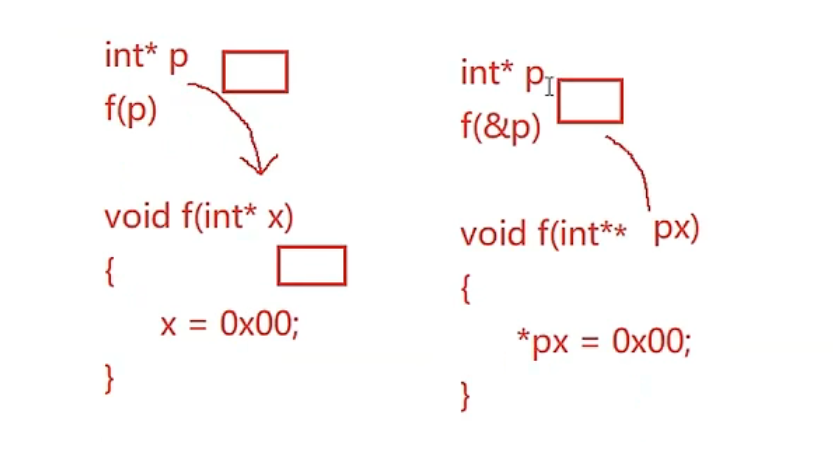
二级指针（通过指针去改变指向空间的内容传一级指针，改变指针的指向传二级指针）

哨兵位的头节点不需要存储有效数据

head=tail=(ListNode*)malloc(sizeof(ListNode));

但是不能直接返回head哨兵位头节点

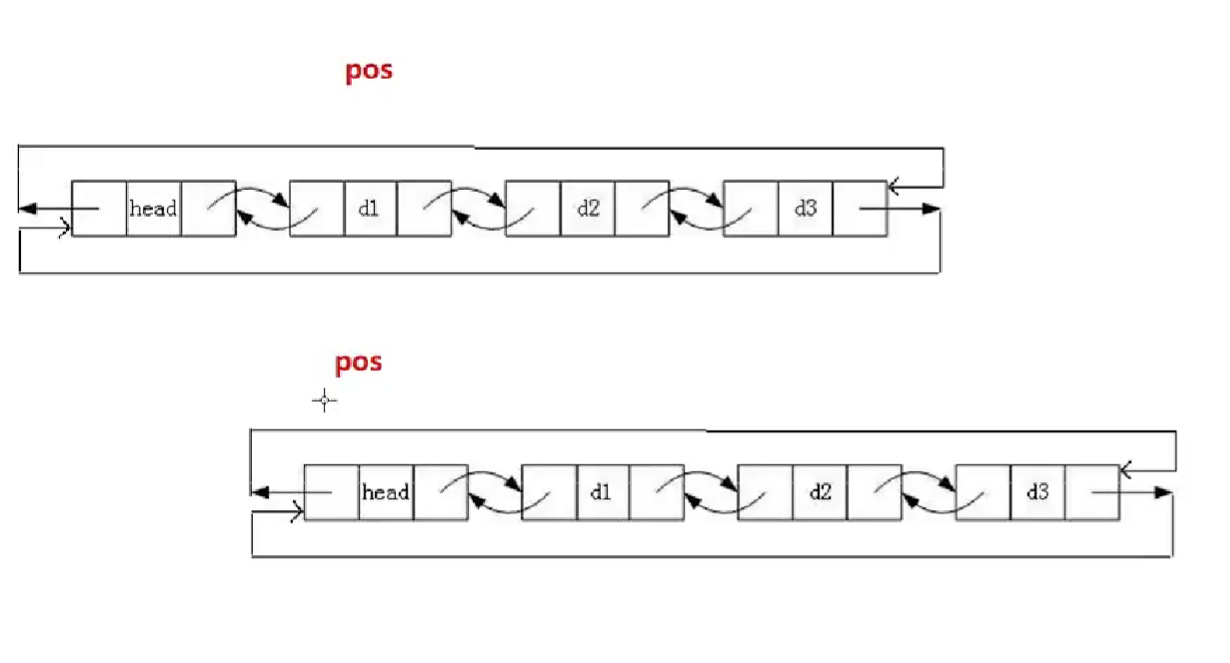
带头的循环链表

//尾插
void ListPushBack(LTNode* phead,LTDataType x)
{
    assert(phead);
    LTNode* tail=phead->prev;
    LTNode* newnode=(LTNode*)malloc(sizeof(LTNode));
    newnode->data=x;
    
    tail->next=newnode;
    newnode->prev=tail;
    newnode->next=phead;
    phead->prev=newnode
}
//尾删
void ListpopBack(LTNode* phead)
{
    //如果继续删除会把哨兵位的头节点也删除所以要加断言
    assert(phead);
    assert(phead->next!=phead);
    LTNode* tail=phead->prev;
    LTNode* tail->prev;
    //先释放会产生野指针问题,所以要记录tail的前一个指针
    free(phead->prev);
    
    tailPrev->next=phead;
    phead->prev=tailPrev;
    
}

//头插 
//phead指向哨兵位的头，next指针指向除了哨兵位的第一个节点

/*LTNode* BuyListNode(LTDateType x)
{
    LtNode* newnode=(LTNode*)malloc(sizeof(LTNode));
    newnode->data=x;
    newnode->next=NULL;
    newnode->prev=NULL;
    return newnode;
}
*/
void ListPushFront(LTNode* phead,LTDateType x)
{
    assert(phead);
    LTNode* newnode=BuyistNode(x);
    LTNode* next=phead->next;
    
    phead->next=newnode;
    newnode->prev=phead;
    
    newnode->next=next;
    next->prev=newnode;
    //如果这个链表是一个空链表也不会有问题(此时phead的prev指向自己，phead的next也指向自己)
}

//头删
void ListPopFront()
{
    assert(phead);
    //链表空
    assert(phead->next!=phead);
    
    LTNode* next=phead->next;//多定义一个变量
    LTNode* nextNext=next->next;//再多定义一个变量，就可以不用管是否先后释放内存
    
    phead->next=nextNext;
    nextNext->prev=phead;
    free(next);
    
}

//找到值为x的节点
LTNode* ListFind(LTNode* phead,LTDateType x)
{
    assert(phead);
    LTNode* cur=phead->next;
    while(cur!=phead)
    {
         if(cur->data==x)
         {
             return cur;
         }
        cur=cur->next;
    }
    return NULL;
}

//pos位置之前插入
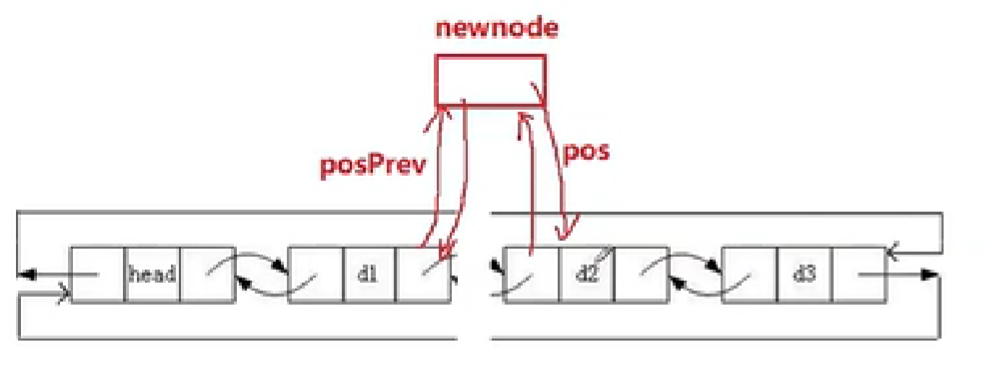
void ListInsert(LTNode* pos,LTDateType x)
{
    assert(pos);
    LTNode* posPrev=pos->prev;
    LTNode* newnode=BuyListNode(x);
    
    posPrev->next=newnode;
    newnode->prev=posPrev;
    newnode->next=pos;
    pos->prev=newnode;
}

在pos位置插入

下图相当于头插尾插

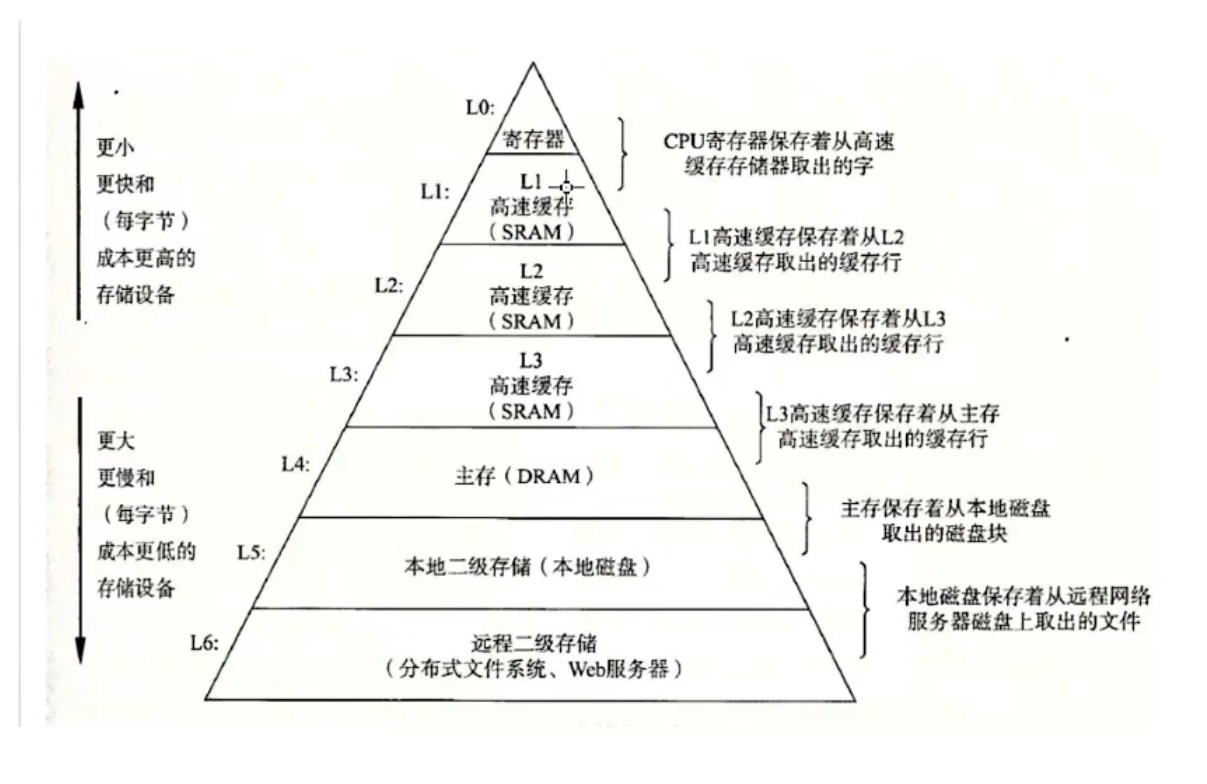
相比于顺序表链表cup命中率不高，有可能造成缓存污染(连续的物理空间造成的)

访问存储数据的内存位置，先看这个地址在不在缓存中，在就直接访问，不在就先加载到缓存再访问（加载到缓存不只加载着一个数据位置，而是预加载就近原则的一片数据内存位置）

栈

进行数据的插入和删除操作的一端称为栈顶，另一端为栈底

//stack.h
typedef int STDateType;
typedef struct Stack
{
    STDataType* a;//栈用数组存储
    int top;
    int capacity;//空间长短
}ST;

void StackInit(ST* ps);
void StackDestory(ST* ps);
void StackPush(ST* ps,STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool SackEmpty(ST* ps);//判断栈是不是为空

//stack.c
//1.
void StackInit(ST* ps)
{
    assert(ps);//结构体指针不能为空
    ps->a=NULL;
    ps->top=0;//ps->top=-1; 初始化时top给的为0，意味着top指向栈顶数据的下一个  初始化时，top给的是-1，意味着top指向栈顶数据
    ps->capacity=0;
}


//2.
void StackPush(ST* ps,STDataType x)
{
    if(ps->pop==ps->capacity)//如果空间已经满了
    {
        int newCapacity=ps->capacity==0?4:ps->capacity*2;//如果空间满了就扩容到之前的二倍，如果初始空间是0就扩容到4
        STDataType* tmp=realloc(ps->a,sizeof(STDataType)*newCapacity);
        if(tmp==NULL)
        {
            printf("realloc fail\n");
            exit(-1);
        }
        ps->a=tmp;
        ps->capacity=newCapacity;
    }
    assert(ps);
    ps->a[ps->top]=x;
}


//3.
void StackDestory(ST* ps)//数据删空了还需要destory因为空间还没释放
{
    assert(ps);
    free(ps->a);
    ps->a=NULL;
    ps->capacity=0;
}


//4.删除数据
void StackPop(ST* ps)
{
    assert(ps);
    assert(ps->top>0);
    ps->top--;
}


//5.栈顶数据
STDataType StackTop(ST* ps)
{
    assert(ps);
    assert(!StackEmpty(ps));//判断是否栈为空
    return ps->a[ps->top-1];//因为初始化top为0
}


//6.
bool StackEmpty(ST* ps)
{
    assert(ps);
    if(ps->top==0)
    {
        return true;//为空
    }
    else
    {
        return false;
    }
}


//7.
int StackSize(ST* ps)
{
    assert(ps);
    return ps->
}

//Text.c
void TextStack()
{
    ST st;
    StackInit(&st);
    
    StackPush(&st,1);
    StackPush(&st,2);
    StackPush(&st,3);
    StackPush(&st,4);
    
    while(!StackEmpty(&st))
    {
        printf("%d",StackTop(&st));
        StackPop(&st);
    }
}

队列

只允许再一端进行插入操作，在另一端就进行删除数据的操作（先进先出）。进行插入操作的一端称为队尾，进行删除一端的操作称为队头。

//queue.h
typedef int QDataType;//int可以写作QDataType
typedef struct QueueNode //队列用的是链表结构,这个结构体代表一个新节点
{
    struct QueueNode* next;
    QDataType data;
}QueueNode;

/*
1.
这里的Queue代表结构体
typedef struct Queue
{
    
}Queue;

2.
这里的Queue代表变量
struct Queue
{
    
}Queue;
*/
typedef struct Queue  
{
    QueueNode* head;
    QueueNode* tail;
}Queue;

void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
void QueuePush(Queue* pq,QDataType x);//队尾插入数据x
void QueuePop(Queue* pq);//对头删除数据
QDataType QueuFront(Queue* pq);//取队头的数据
QDataType QueuBack(Queue* pq);//取队尾的数据
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);

//queue.c
//1.
void QueueInit(Queue* pq)
{
    arrert(pq);
    qp->head=NULL;
    pq->tail=NULL;
}


//2.
void QueueDestory(Queue* pq)
{
    assert(pq);
    QueueNode* cur=pq->head;
    while(cur!=NULL)
    {
        QueueNode* next=pq->next;
        free(cur);
    }
}


//3.
void QueuePush(Queue* pq,QDataType x)
{
    assert(pq);
    QueueNode* newnode=(QueueNode*)malloc(sizeof(QueueNode));
    newnode->data=x;
    newnode->next=NULL;
    
    if(pq->head==NULL)
    {
        pq->head=pq->tail=newnode;
    }
    else
    {
        pq->tail->next=newnode;
        pq->tail=newnode;
    }
}


//4. 
void QueuePop(Queue* pq)
{
    assert(pq);
    assert(QueueEmpty(pq));
    QueueNode* next=pq->head->next;
    free(pq->head);
    pq->head=next;
    //tail可能为野指针
    if(pq->head==NULL)
    {
        pq->tail=NULL;
    }
}
           
           
//5.
bool QueueEmpty(Queue* pq)
{
    assert(pq);
    return pq->head==NULL;
}


//6.
int QueueSize(Queue* pq)
{
    assert(pq);
    int n=0;
    QueueNode* cur=pq->head;
    while(cur)
    {
        ++n;
        cur=cur->next;
    }
    return n;
}

//text.c
void TextQueue1()
{
    Queue q;
    QueueInit(&q);//改变一级就传二级，改变结构体就传结构体的指针
    QueuePush(&q,1);
    QueuePush(&q,2);
    QueuePush(&q,3);
    QueuePush(&q,4);
    
    while(!=QueueEmpty(&q))
    {
        QDataType front=QueueFront(&q);
        printf("%d",front);
        QueuePop(&q);
    }
}

int main()
{
    void TextQueue1();
    return 0;
}

串数组和广义表

子串：一个串中任意个连续字符组成的子序列称为子串

子串：子串第一个字符在主串中的位置

串相等：当且仅当两个串的长度相等并且各个对应位置上的字符都相同时，这两个串才是相等的 所有的空串都是相等的