OJ题

1.IO型:自己写头文件，main函数等等

测试用例：我们要去scanf获取

结果：用printf输出

2.接口型（实现已知函数）：不需要写头文件，主函数，提交了以后，会跟oj服务器上他准备好的代码合并

测试用例：通过参数传过来

结果：一般通过返回值拿的，也有可能是输出性参数

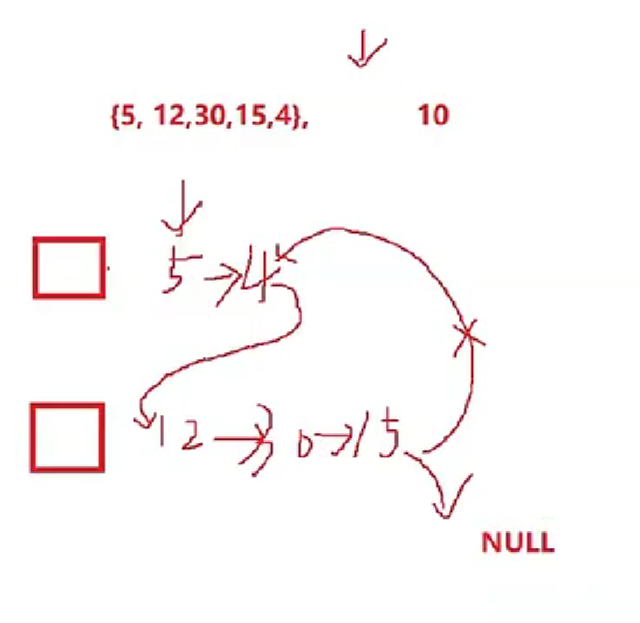
一个整形数组nums里除两个数字以外，其它数字都出现了2次，请写程序找出这两个只出现一次的数据

1
2
3
4
5
6
7
8
9
//C语言不支持返回两个值
//例如输入：nums=[4,1,4,6]  输出：[1,6]或者[6,1]
int* singleNumbers(int8 nums,int numsSize,int * returnSize)//这个returnSize就叫输出型参数
{
    *returnSize=2;//把返回数组的大小给他
    int* arr=(int*)malloc(sizeof(int)*2);
    
    return arr;
}

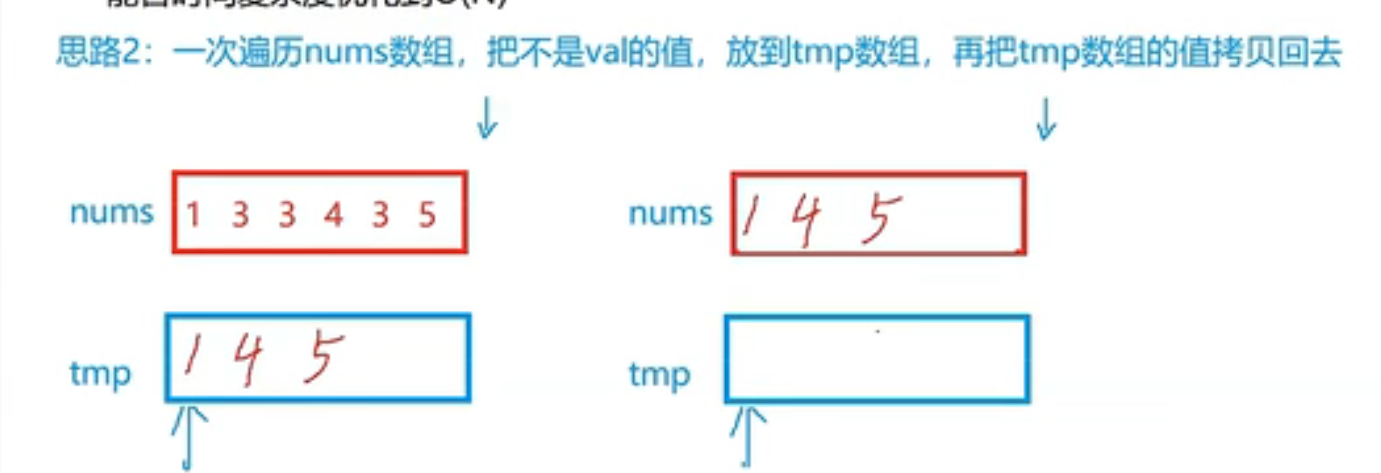
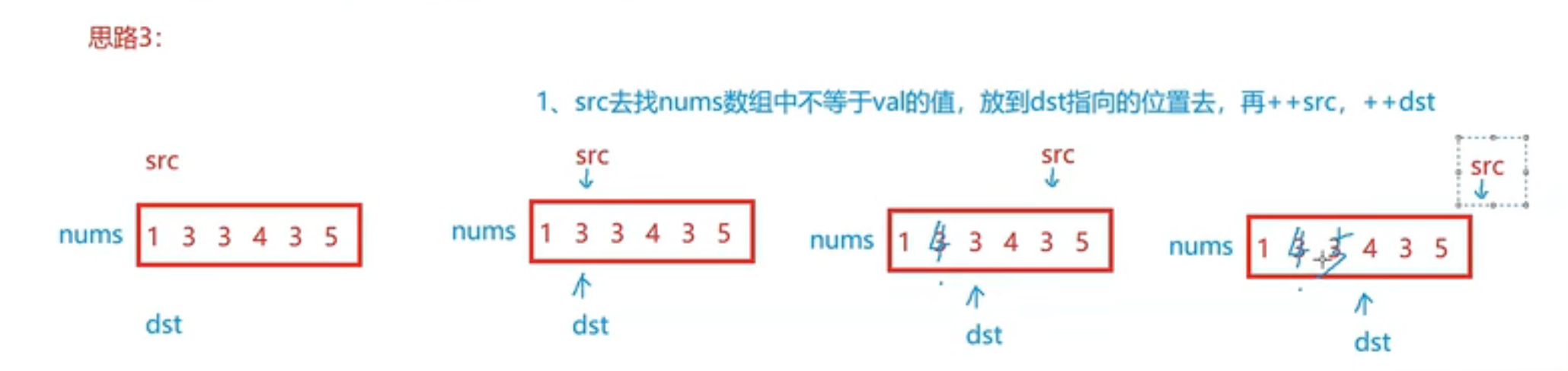
给你一个数组nums和一个值val，你需要原地溢出所有数值相等于val的元素，并返回移除后数组的新长度

1
2
3
4
5
6
7
8
9
/*
1.遇到和val相同的数组元素时，将其后所有元素向前移一位覆盖，找到所有的val，依次挪动数据覆盖删除。时间复杂度为O(n^2)最坏的情况数组中大部分值甚至全部都是val[(n-1)+(n-2)+...]
*/
/*
2.建立一个temp数组，把不是val的值放在temp数组中，再把temp数组的值拷贝回去O(n)
*/
/*
3.定义src和dst为数组下标，用src找不等于 val的值(等于val dst不动，src继续向后找)，放到dst指向的位置中去，再++src，++dst。因为是常数个数所以可以认为O(1)
*/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int removeElement(int* nums,int numSize,int val)
{
    int src=0,dst=0;
    while(src<numSize)
    {
        if(nums[src]!=val)
        {
            nums[dst]=nums[src]; 
            src++;
            dst++;
        }
        else
        {
            src++;
        }
    }
    return dst;
}

去重，删除有序数组中的重复数字（双指针的变形）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
输入：nums=[1,1,2]
输出：2，nums=[1,2]
解释：函数应返回新长度2，并且原数组nums的前两个元素被修改为1，2。。不需要考虑数组中超出新长度后面的元素
*/
 int removeDuplicates(int* nums,int numsSize)
 {
     if(numsSize==0)
         return 0;
     int i=0,j=1;
     int dst=0;
     while(j<numsSize)
     {
         if(nums[i]==nums[j])
         {
             ++j;
         }
         else
         {
             nums[dst]=nums[i];
             ++dst;
             i=j;
             j++
         }
     }
     nums[dst]=nums[i];
     ++dst;
     return dst;
 }
//下图为两种情况[0,0,1,1,1,2,2,3,3,4]和[0,0,1,1,2,2,3,3]

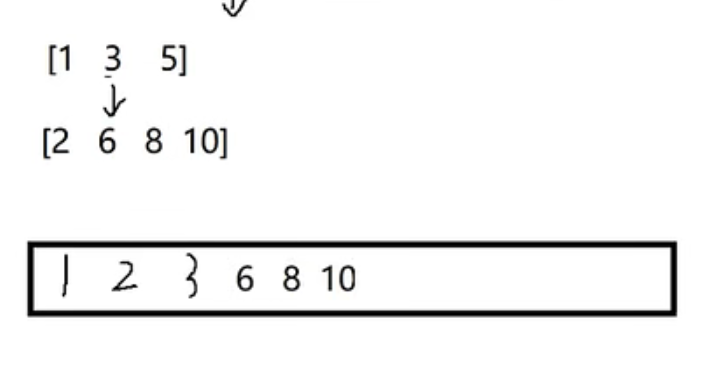
合并两个有序数组（归并排序）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
有序数组：非递减数组
输入：nums1=[1，2，3，0，0，0]，m=3,nums2=
[2,5,6]
输出：[1,2,2,3,5,6]
注意：最终，合并后的数组不应由函数返回，而是存储在数组num1中，为了应对这种情况，num1的初始长度为m+n，其中前m个元素表示应合并的元素，后n给元素为0，应忽略num2的长度为n
*/
void merge(int* nums1,int nums1Size,int m,int* nums2,int nums2Size,int n)
{
    int end1=m-1,end2=n-1;
    int end=m+n-1;
    while(end1>=0 && end2>=0)
    {
        if(nums[end1]>nums2[end2])//num1大就把nums1的数据放end所对应的数组元素上，nums2数据大就把nums2的数据放end所对应的数组元素上
        {
            nums1[end]=nums1[end1];
            --end2;
            --end1;
        }
        else
        {
            nums1[end]=nums2[end2];
            --end2;
            --end1;
        }
    }
    while(end2>=0)//不可能同时结束,当nums2先结束时（图1），不用做后续处理;另一种情况(合并[2,2,3,0,0,0]和[1,1,6])时是num1先结束就要把nums2的剩余数据赋值给nums1
    {
        nums1[end]=nums[end2];
        --end2;
        --end;
    }
}

图2

此题是从后往前放数据从大到小开始放;而归并排序是从小到大比较从前往后放，并且归并排序是生成一个新数组存放排过序的元素

1
2
3
4
//归并排序
[1,3,5]
[2,6,7,8]
//给两个指针分别指向两个数组的起始元素进行比较，小的放入第三个数组，并且这个数对应的指针++,再继续比较两个指针所指向的元素大小，把小元素的继续放在第三个数组中，再++它所对应的指针

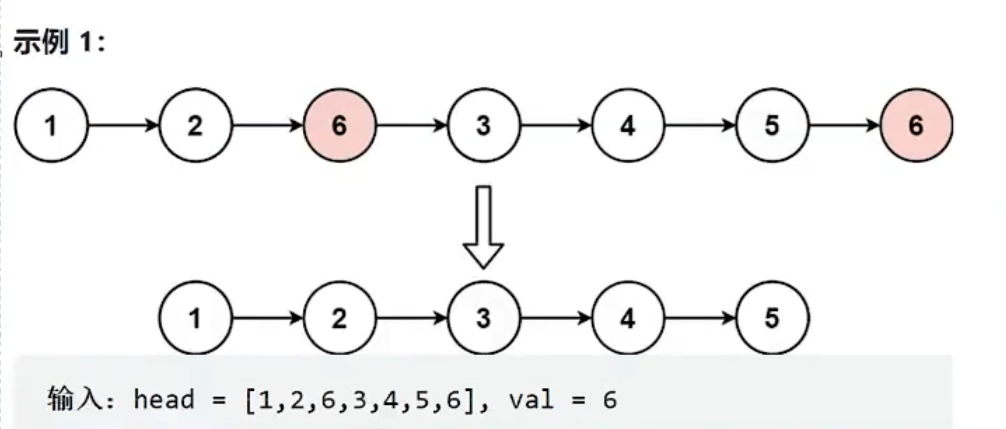
移除链表元素（给你一个链表的头节点head和一个整数val，请你删除链表中所有满足Node.val==val的节点，并返回新的头节点）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct ListNode* removeElement(struct ListNode* head,int val)
{
    struct Listnode* prev=NULL,*cur=head;
    while(cur)
    {
        //当第一个都需要删除(头删)的时候就会报错例如[7，7，7，7]  7
        if(cur->val==val)
        {
            //头删
            if(cur==head)
            {
                head=cur->next;//head指向下一个节点
                free(cur);//删除第一个节点
                cur=head;//删除完的第一个就是当前head指向的节点，再给cur
            }
            else
            {
                //中间删除
                prev->next=cur->next;
                free(cur);
            
                cur=prev->next;
            }
        }
        else
        {
            //迭代往后走
            prev=cur;
            cur=cur->next;
        }
            
    }
    return head;
}

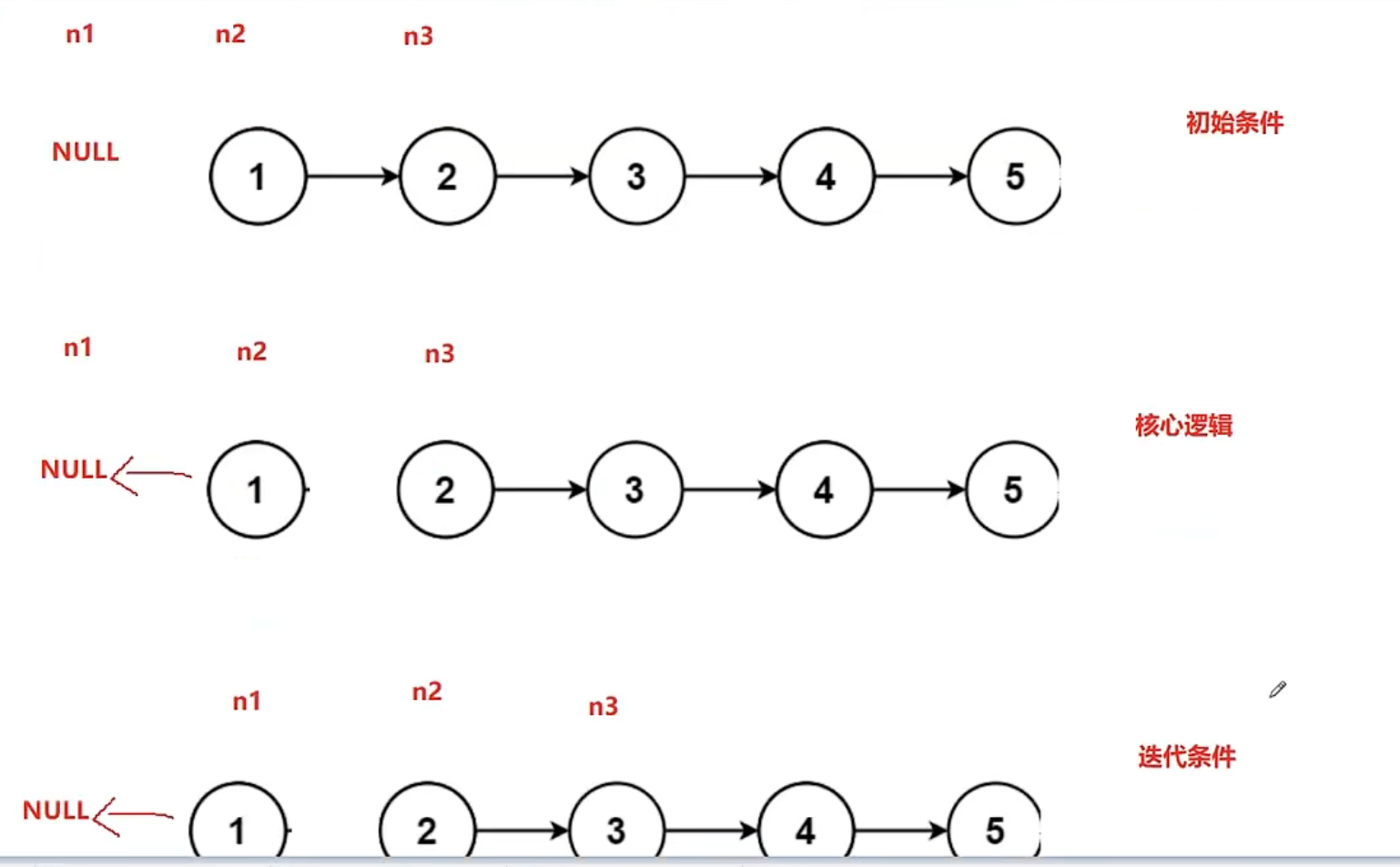
翻转链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
struct ListNode* reverseList(struct ListNode* head)
    //n1,n2用来翻转n3用来记录下一个节点，方便迭代的
{
    //如果链表为空就不需要翻转
    if(head==NULL)
        return NULL;
    struct ListNode* n1,n2,n3;
    n1=NULL;
    n2=head;
    n3=head->next;
    while(n2)
    {
        //翻转
        n2->next=n1;
        //迭代往后走
        n1=n2;
        n2=n3;
        //当n2为空时n3没有办法指向下一个节点因为之前n3已经为空
        if(n3!=NULL)
            n3=n3->next;
    }
    return n1;
}

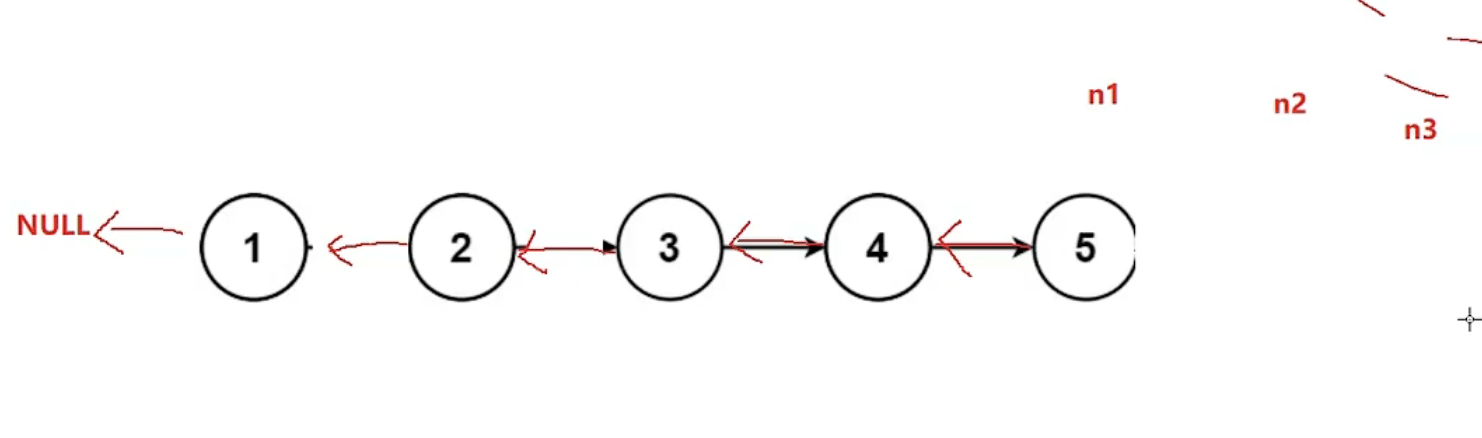
上图为基本翻转逻辑，下图为for循环结束条件图示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//第二种算法:取原链表中节点，头插到newhead新链表中
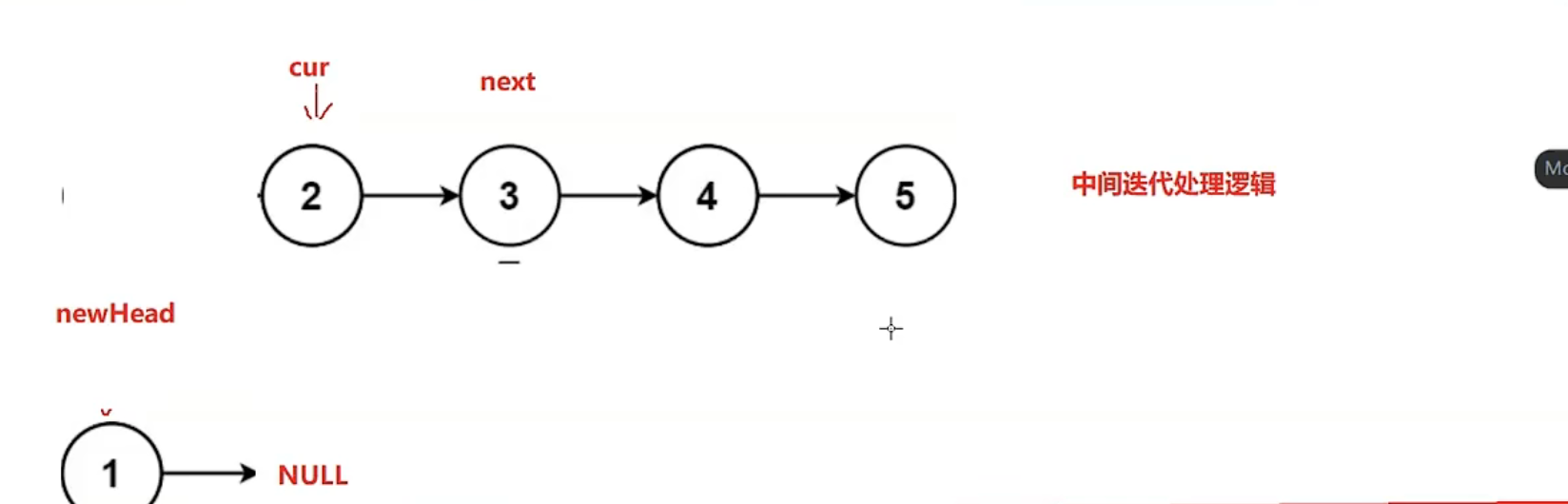
struct ListNode* reverseList(struct ListNode* head)
{
    struct ListNode*cur=head;
    struct ListNode* newhead=NULL;
    while(cur)
    {
        struct ListNode* next=cur->next; 
        //头插
        cur->next=newhead;
        newhead=cur;
        //迭代往后走
        cur=next;
    }
    return newhead;
}

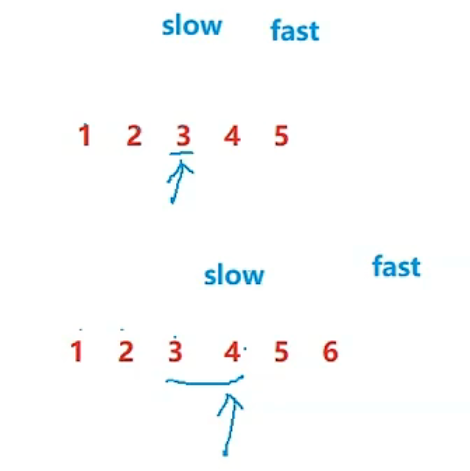
返回链表的中间节点(如果有两个中间节点则返回第二个中间节点) 要求:只能遍历链表一次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//快慢指针问题:定义两个指针一个快指针fast一个慢指针slow，fast每次走两步，slow每次走一步，如果是奇数个数字fast走到最后一个数字的后一个指向空此时slow为第二个中间节点；如果是偶数给数字fast走到最后一个时slow正好走到中间节点
struct ListNode* middleNode(struct ListNode* head)
{
    struct ListNode* slow,*fast;
    slow=fast=head;
    while(fast&&fast->next)//当发射台走到最后或者走到NULL时停止
    {
        slowslow->next;
        fast=fast->next->next;
    }
    return slow;
}

//变形：求链表倒数第K个节点
/*
1.先让fast走k步；slow和fast再一起走，fast==NULL时，slow为倒数第k个节点
2.先让fast走k-1步，slow和fast再一起走，fast->==NULL时，slow为倒数第k个节点
*/


//1.
struct ListNode* FindKthToTail(struct ListNode* plistHead,int k)
{
    struct ListNode* fast,*slow;
    slow=fast=plistHead;
    while(k--)//循环k次
    //while(--k)//循环k-1次
    {
        fast=fast->next;
        //k大于链表的长度 当{1,2,3,4,3,2}，k=30时
        if(fast==NULL)
        {
            retuen NULL;
        }
    }
    while(fast)
    {
        slow=slow->next;
        fast=fast->next;
    }
    return slow;
}

上图为变形前的示意图

合并两个有序列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
//用返回值的方式就不需要用二级指针
struct ListNode* mergeTwoLists(struct ListNode* l1,struct ListNode* l2)
{
    //当其中一个链表为空，就返回另一个链表
if(l1==NULL)
    return l2;
if(l2==NULL)
    return l1;
struct ListNode* head=NULL,*tail=NULL;
while(l1&&l2)
{
    if(li->val<l2->val)
    {
        if(head==NULL)
        {
            head=tail=l1;
        }
        else
        {
            tail->next=l1;
            tail=tail->next;
        }
        l1=l1->next;
    }
    else
    {
        if(head==NULL)
        {
            head=tail=l2;
        }
        else
        {
            tail->next=l2;
            tail=tail->next;
        }
        l2=l2->next;
    }
    //当某一个链表结束的时候把另外一个链接，由于不知道哪一个先结束于是用两个if语句
    if(l1)
    {
        tail->next=l1;
    }
    if(l2)
    {
        tail->next=l2;
    }
    return head;//fan'hui
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
if(l1==NULL)
    return l2;
if(l2==NULL)
    return l1;
struct ListNode* head=NULL,*tail=NULL;
//哨兵位的头节点
head=tail=(struct ListNode*)malloc(sizeof(struct ListNode));
while(l1&&l2)
{
    if(li->val<l2->val)
    {
        tail->next=l1;
        tail=tail->next;
        l1=l1->next;
    }
    else
    {
        tail->next=l2;
        tail=tail->next;
        l2=l2->next;
    }
}
    if(l1)
    {
        tail->next=l1;
    }
    if(l2)
    {
        tail->next=l2;
    }

//不能直接返回哨兵位的头，要释放哨兵位的头，返回哨兵位的next
struct ListNode*list=head->next;
free(head);
return list;

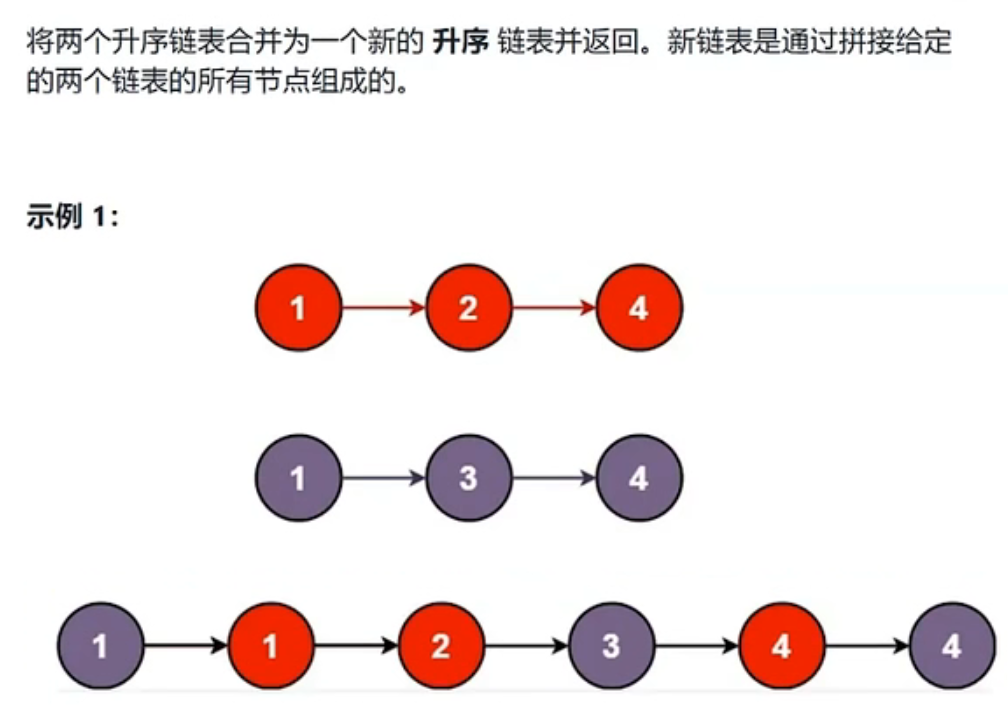
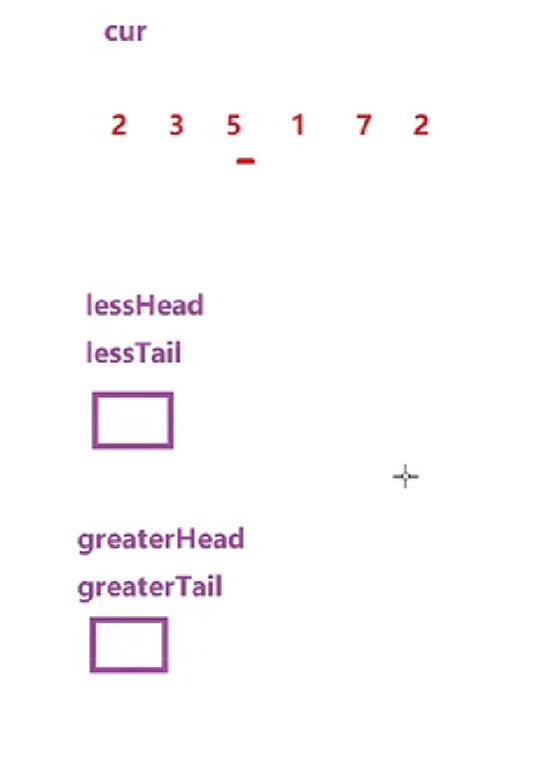
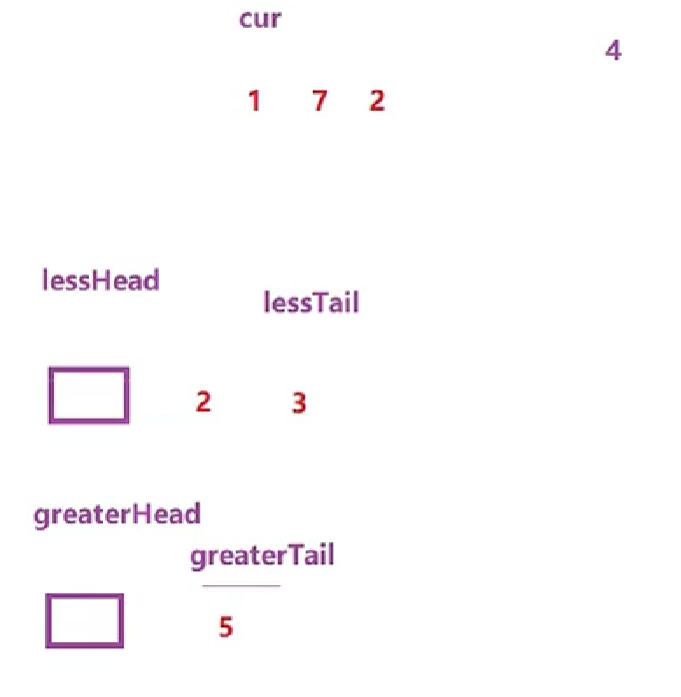
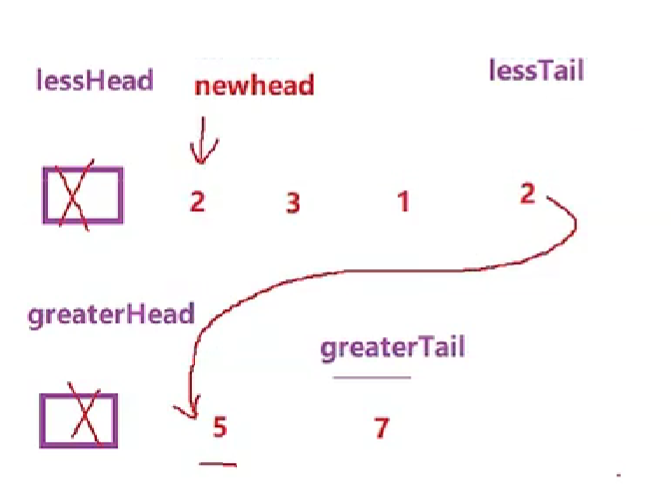
链表的分割(现在有一链表的头指针ListNode* pHead,给一定值x，编写一段代码将所有小于x的节点排在其余节点之前，且不能改变原来的数据顺序，返回重新排列后的链表的头指针)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//eg:2  3  5  1  7  2    x=4
//结果:2 3 1 2 5 7


//新定义两个链表，把比x小的放尾插在第一个链表中，把大于x的尾插在第二个链表中再把这两个链表链接
ListNode* partition(ListNode* pHead,int x)
{
    struct ListNode* lessHead,*lessTail,*greaterHead,*greaterTail;
    //开一个哨兵位，方便尾插
    lessHead=lessTail=(struct ListNode*)malloc(sizeof(strcut ListNode*));
    lessTail->next=NULL;
    greaterHead=lessTail=(struct ListNode*)malloc(sizeof(strcut ListNode*));
    greaterTail->next=NULL;
    
    struct ListNode* cur=pHead;
    while(cur)
    {
        if(cur->val<x)
        {
            lessTail->next=cur;
            lessTail=cur;
        }
        else
        {
            greaterTail->next=cur;
            greaterTail=cur;
        }
        cur=cur->next;
    }
    //链接两个链表less和greater
    lessTail->next=greaterHead->next;
    
    //防止无限循环
    greater->next=NULL;
    
    //free两个哨兵节点，但是free之后就无法返回新链表(less和greater连接过后的链表)的头节点，所以需要提前记录lessHead的下一个节点
    struct ListNode* newHead=lessHead->next;
    free(lessHead);
    free(greaterHead);
    
    return newhead;
    
}
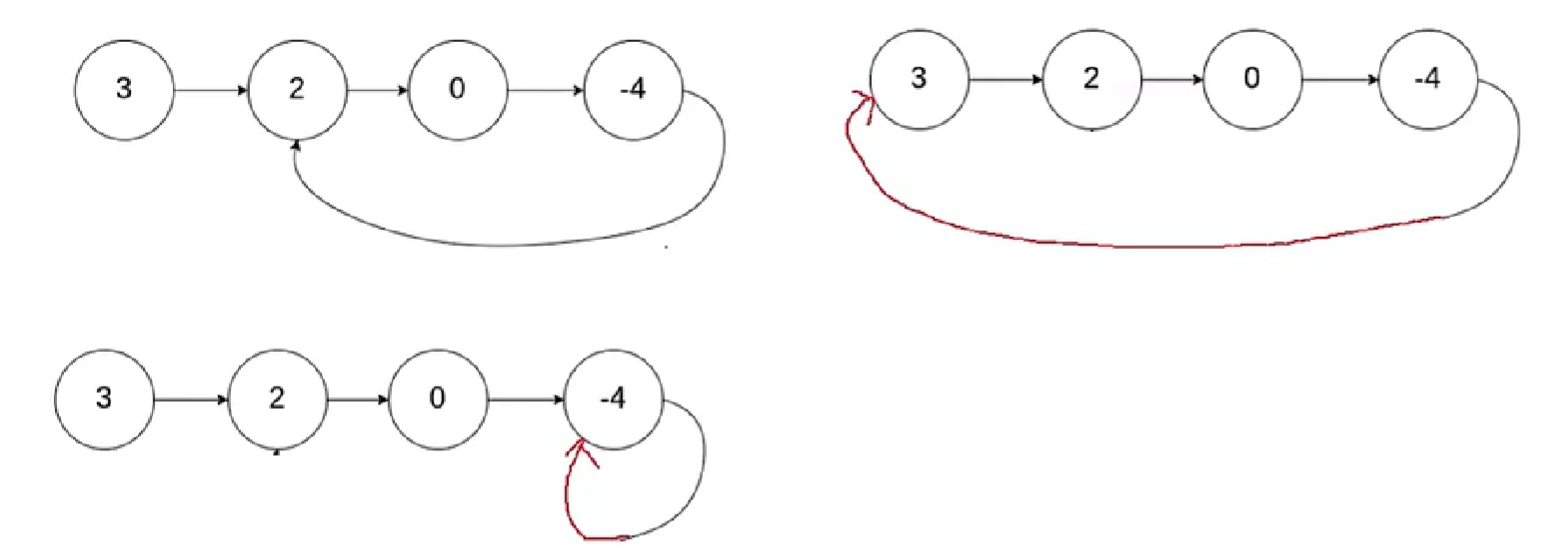
图一：初始步骤

图二：逻辑步骤

图三：逻辑结束

报错原因：

15本来指向4，现在4又指向12，无限循环，内存会超

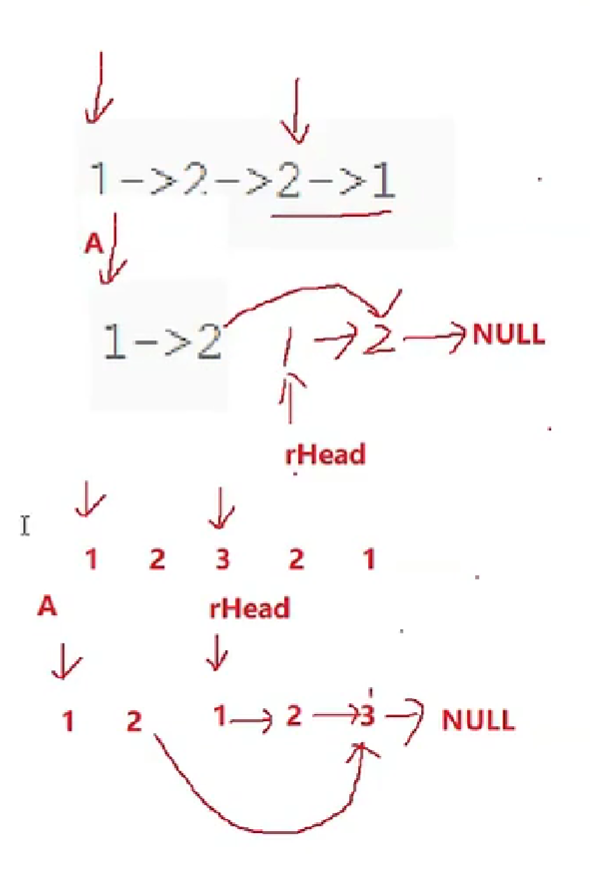
链表的回文结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构，给定一个链表的头指针A，请返回一个bool值，代表其是否为回文结构，保证链表长度小于等于900
//例如：1->2->2->1  返回:true


//方法:把后半部分逆置(翻转)，然后用前半部分和后半部分进行比较(不用把前后两部分断开)

struct ListNode* middleNode(struct ListNode* head)
{
    struct ListNode* mid=middleNode(A);//之前题目的代码，找到中间节点
    struct ListNode* rHead=reverseList(mid);//之前题目的代码，翻转链表从mid开始
    
    struct ListNode* curA=A;
    struct ListNode* curR=rHead;
    while(curA && curR)
    {
        if(curA->val!=curR->val)
        {
            return false;
        }
        else
        {
            curA=curA->next;
            curR=curR->next;
        }
    }
}

不用断开原因本来中间的2就指向末尾的3(奇数情况)，本来中间的2就指向末尾的1(偶数情况)

链表相交(一个节点只有一个next，只能聚合不能分散 )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//1.判断两个链表是否相交  2.如果相交，求交点
//方法1: 依次取A链表中的每个节点跟B链表中的所有节点比较，如果有地址相同的节点，就是相交，第一个相同的就是交点    方法2: 尾节点相同就相交，否则就不相交 求焦点:长的链表先走长度差，再同时走，第一个相同就是焦点

//方法2实现如下：
struct ListNode *getIntersectionNode(struct ListNode *headB)
{
    struct ListNode* tailA=headA;//不用headA去迭代的原因是不方便找头
    struct ListNode* tailB=headB;
    int lenA=1;
    while(tailA->next)
    {
        ++lenA;//算出A链表的长度
        tailA=tail->next;
    }
    
    int lenB=1;
    while(tailB->next)
    {
        ++lenB;//算出B链表的长度
        tailB=tailB->next;
    }
    //不相交
    if(tailA!=tailB)
    {
        return NULL;
    }
    int gap=abs(lenA-lenB);//两个链表的差距gab,abs是绝对值的意思
    struct ListNode* longList=headA;//假设A长B短
    struct ListNode* shortList=headB;
    if(lenA<lenB)
    {
        shortList=headA;
        longList=headB;
    }
    //长的先走gap步
    while(gap--)
    {
         longList=longList->next;
    }
    
    while(longList!=shortList)
    {
        longList=Longlist->next;
        shortList=shortList->next;
    }
    retuen longList; 
}

环形链表

带环的三种情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//1.是否带环  2.找出带环链表的入口节点
/*
slow和fast指向链表的开始，slow一次走一步，fast一次走两步，不带环fast就会走向空，带环，fast就会在环里追上slow(zhui'ji)
*/

//1.
bool hasCycle(struct ListNode *head)
{
    struct ListNode* slow=head,*fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            return true;
        }
    }
    return NULL;
}


//2.
//一个指针从相遇点开始走，一个指针从链表头开始走，它们会在环的入口点相遇

/*
追上相遇的过程中，慢指针走的距离:L+X;快指针走到距离:L+n*X+C(C为环的长度，n是他们相遇之前，fast在环里面走的圈数，n>=1)
在相遇时，慢指针不可能走在环内超过一圈，因为此时快指针已经走两圈了

快指针走的路程是慢指针的二倍
2(L+X)=L+n*C+X
L+X=n*C
L=n*C-X
L=(n-1)*C+C-X

(n-1)*C指的是整数倍圈，相当于从meetNode又走到meetNode
C-X指的是从meetNode走到环入口点
所以 L=(n-1)*C+C-X 指的是一个指针从相遇点开始走，一个指针从链表头开始走，它们会在环的入口点相遇
*/

struct ListNode *detectCycle(struct ListNode* head)
{
    struct ListNode* slow=head,*fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            //相遇
            struct ListNode* meet=slow;
            //一个指针从相遇点开始走，一个指针从链表头开始走，它们会在环的入口点相遇     公式证明，看上面讲解
            while(meet!=head)
            {
                meet=meet->next;
                head=head->next;
            }
            return meet;
        }
    }
    return NULL;
}
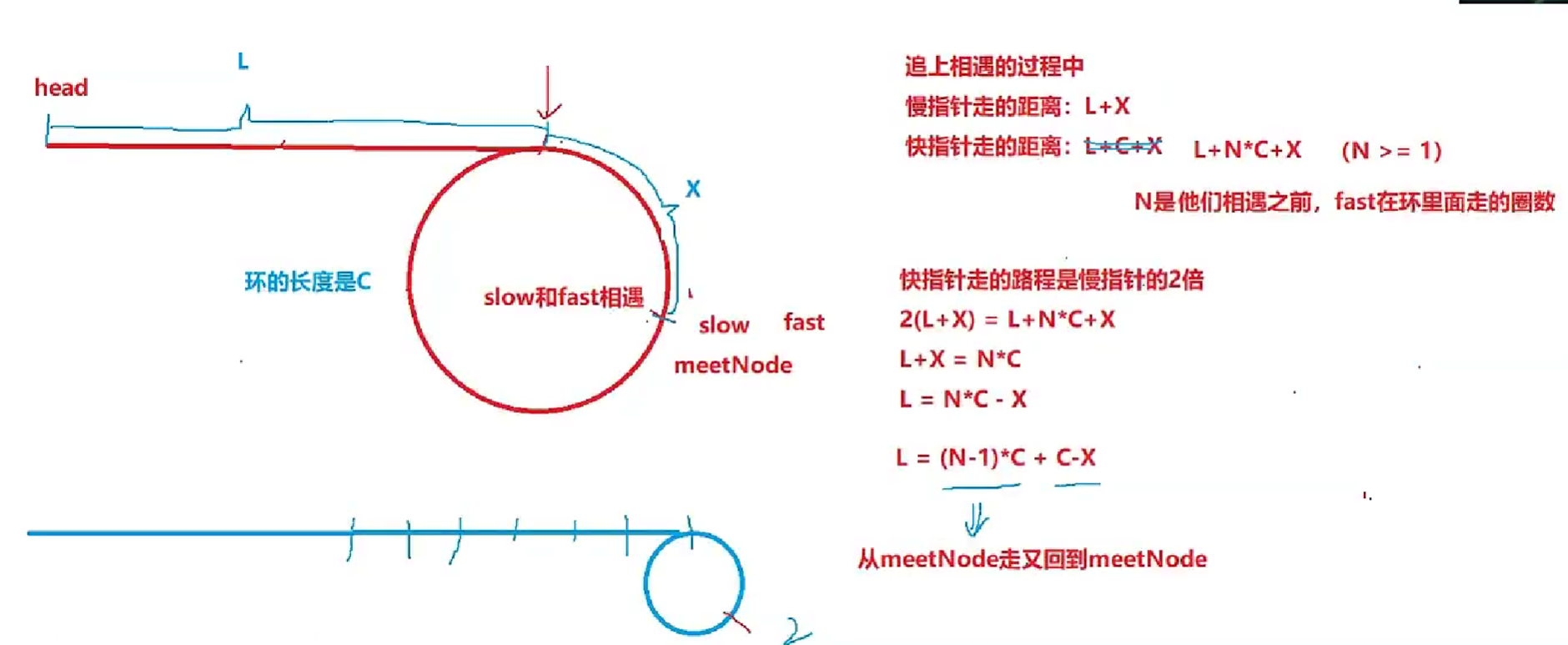
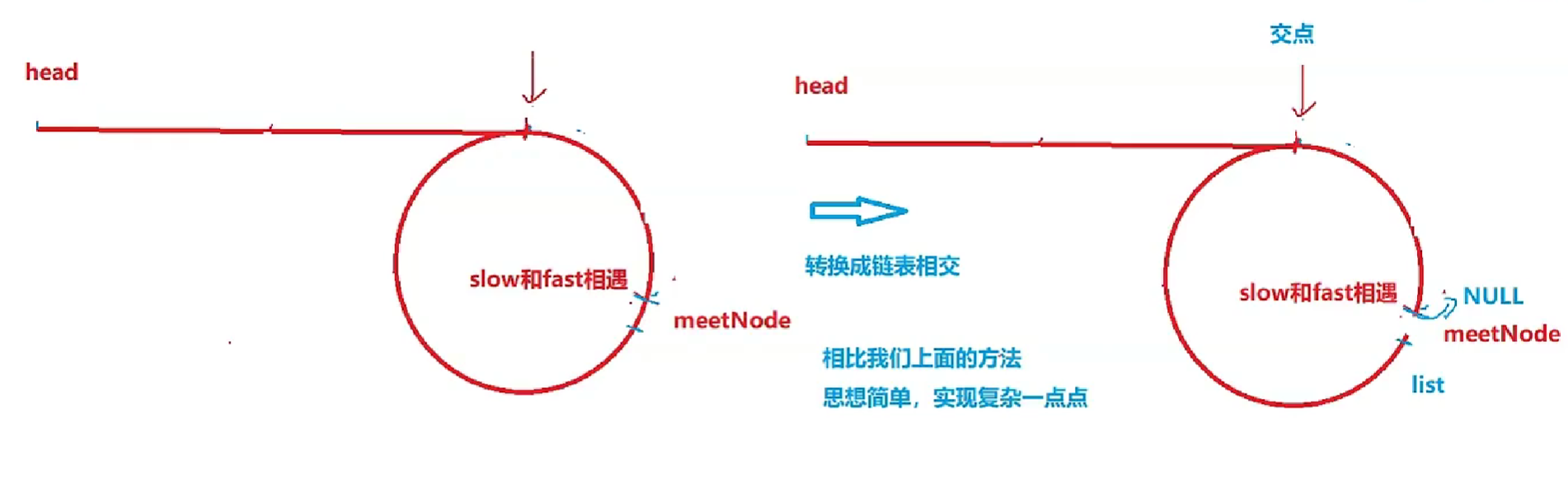
延伸问题：
1.为什么slow和fast一定会在环中相遇？会不会在环里面错过，永远遇不上？ 不会
  • 第一步：slow和fast，fast一定先进环，这时slow走了入环前距离的一半
  • 第二步：随着slow进环，fast已经在环里面走了一段，走了多少跟环的大小有关，假设slow进环的时候，slow跟fast的距离是N，fast开始追slow，slow每往前走一步，fast每次往前走两步，每追一次fast和slow的距离变化为N ,N-1,N-2,N-3,......,1,0 所以会相遇
2.为什么slow走一步，fast走两步？fast能不能一次走3，4，5...n？ 结论：不一定会相遇
  • 以fast走三步为例子
    • N为偶数，每追一次fast和slow的距离变化为N ,N-1,N-2,N-3,......,1,0可以追上
    • N为奇数 ，每追一次fast和slow的距离变化为N ，N-2,N-4,N-6,......,1,-1这一次追不上。距离变成-1意味着他们之间的距离变成C-1(C是环的长度)
      • 如果C-1是奇数，那么就永远追不上了，陷入死循环
      • 如果C-1是偶数，那么就可以追上

图一解决第一问

图二解决第二问

图三是第二个问题的第二种方法，转换为链表相交问题（相遇点下一个点为第二个链表的头节点，把相遇点滞空）

复制带随机指针的链表（复杂链表的复制）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
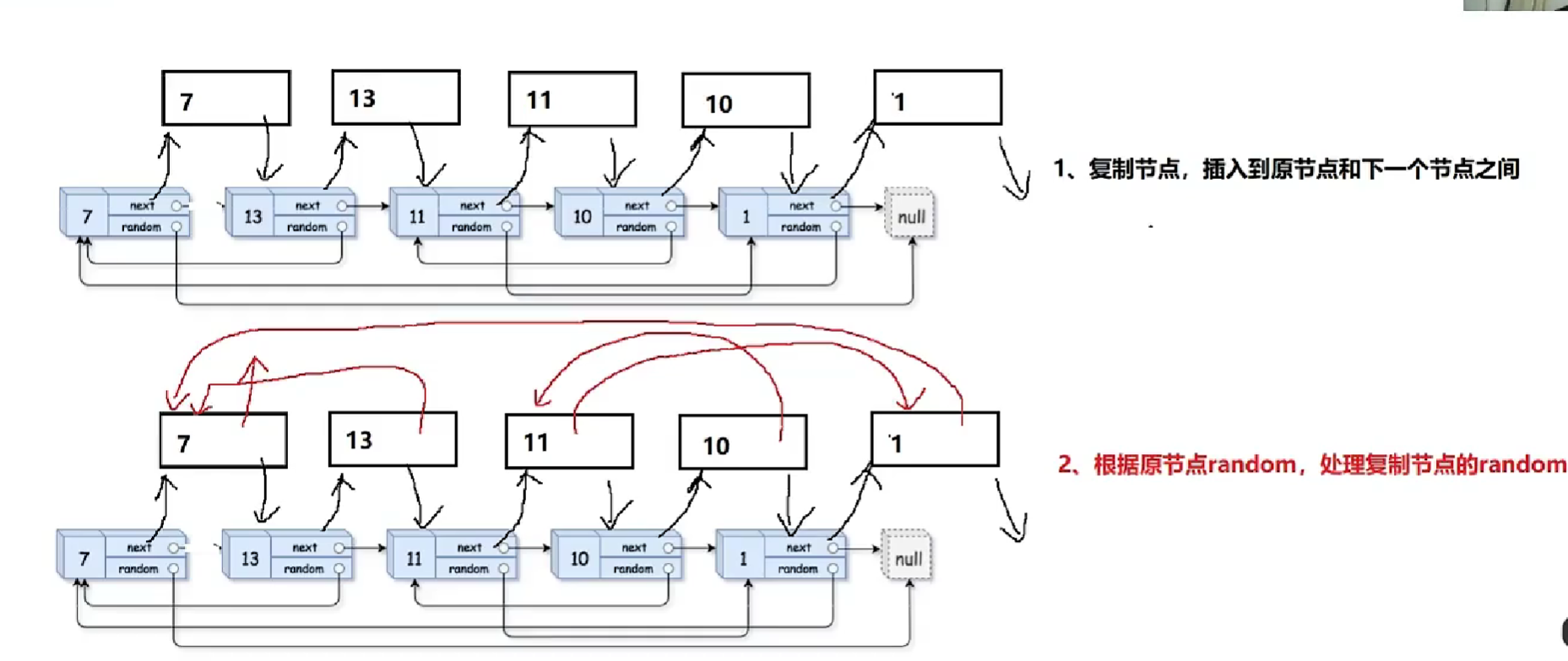
//给你一个长度为n的链表，每个节点包含一个额外增加的随机指针random，该指针可以指向链表中的任何节点或空节点

struct Node* copyRandomList(struct Node* head)
{
    //1.拷贝节点插入原节点后面
    struct Node* cur=head;
    while(cur)
    {
        struct Node* copy=(struct Node*)malloc(sizeof(struct Node));
        copy->val=cur->val;
        //插入copy节点
        copy->next=cur->next;
        cur->next=copy;
        
        cur=copy->next;
    }
    
    //2.根据原节点处理copy节点的random节点
    cur=head;//重新让cur指向头节点开始迭代
    while(cur)
    {
        struct Node* copy=cur->next;
        if(cur->random==NULL)//如果被copy的指针的random指向空
        {
            copy->random=NULL;
        }
        else
        {
            copy->random=cur->random->next;
        }
        cur=copy->next;
    }
    
    //3.复制节点解下来链接成一个新链表，恢复原链表链接关系
    struct Node* copyHead=NULL,*copyTail;
    cur=head;
    while(cur)
    {
        struct Node* copy=cur->next;
        struct Node* next=copy->next;
        if(copyTail==NULL)
        {
            copyHead=copyTail=copy;
        }
        else
        {
            copyTail->next=copy;
            copyTail=copy;
        }
        
        cur->next=next;
        
        cur=next;
    }
    return head;
}

3.复制节点解下来链接成一个新链表，恢复原链表链接关系

有效的括号 给定一个只包括‘（’ ，‘）’ ，‘[’ ,']' ,'{' ，‘}’的字符串s，判断是否有效 1.左括号必须和相同类型的右括号闭合2.左括号必须以正确的顺序闭合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//左括号入栈,右括号取栈顶元素(括号)和这个右括号比较
bool isValid(char* s)
{
    ST st;
    StackInit(&st);
    while(*s)
    {
        if((*s=='(' )
            || (*s=='[')
            || (*s=='{'))
        {
            StackPush(&st,*s);//左括号入栈
            ++s;
        }
        else//如果此时指针s指向右括号
        {
            //遇到右括号了但栈里面没有数据，说明前面没有左括号，不匹配返回false    [[]]]或者]
            if(StackEmpty(&st))
            {
                return false;
            }
            
            
            STDataType top=StackTop(&st);//把栈顶数据复制给变量top
            StackPop(&st);//删除栈顶数据，让可以被右括号匹配的左括号依次出栈
            if(*s==')'&&top！='(' || *s==']'&&top！='[' || *s=='}'&&top！='{')//不匹配
            {
                StackDestory(&st);//注意释放空间
                return false;
            }
            else//匹配
            {
                ++s;
            }
        }
    }

    //如果栈不是空，说明栈中还有左括号未出
    //没有匹配返回的是false
    bool ret=StackEmpt(&st);
    
    StackDestory(&st);
    return true;
}

请你仅使用两个队列实现一个后入先出的栈，并支持普通栈的全部四种操作(不能改变队列的结构只能去调用队列提供的接口去实现)

  • void push(int x)将元素x压入栈顶
  • int pop( )移除并返回栈顶元素
  • int top( )返回栈顶元素
  • boolean empty( )如果栈是空的，返回true；否则返回false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
 //入数据，往不为空的队列入，保持另一个队列为空;出数据，依次出队头的数据，转移到另一个队列保存，只剩最后一个时，pop掉
MyStack* myStackCreate()
{
    MyStack* st=(Mystack*)malloc(sizeof(MyStack));
    QueueInit(&st->q1);//初始化第一个队列
    QueueInit(&st->q2);
    return st;
}

//哪个队列不为空就往这个队列入数据
void myStackPush(MyStack* obj,int x)
{
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

//出数据
int MyStackPop(MyStack* obj)
{
    Queue* emptyQ=&obj->q1;
    Queue* noneemptyQ=&obj->q2;
    if(!QueueEmpty(&obj->q2))
    {
        emptyQ=&obj->q1;
        noneemptyQ=&obj->q2;
    }
    
    //非空队列的数据导入空队列直到还剩一个
    while(QueueSize(noneemptyQ)>1)
    {
        //把队头的数据依次添加到队列2(这时队列1中还有数据)，并且把队列1的数据删除。QueueFront找队头数据，QueuePush导数据
        QueuePush(emptyQ,QueueFront(noneempty(Q)));
        QueuePop(noneemptyQ);
    }
    //保存最后一个数据
    int top=QueueFront(noneemptyQ);
    //删除队1最后一个数据
    QueuePop(noneemptyQ);
    
    return top;
}


//队列不仅可以取队头也可以取队尾，就是只能删队头不能删队尾
int MyStackTop(Mystack* obj)
{
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q2);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}



bool myStackEmpty(MyStack* obj)
{
    //队列q1和q2都不为空
    return QueueEmpty(&obj->q1)&& QueueEmpty(&obj->q2);
}

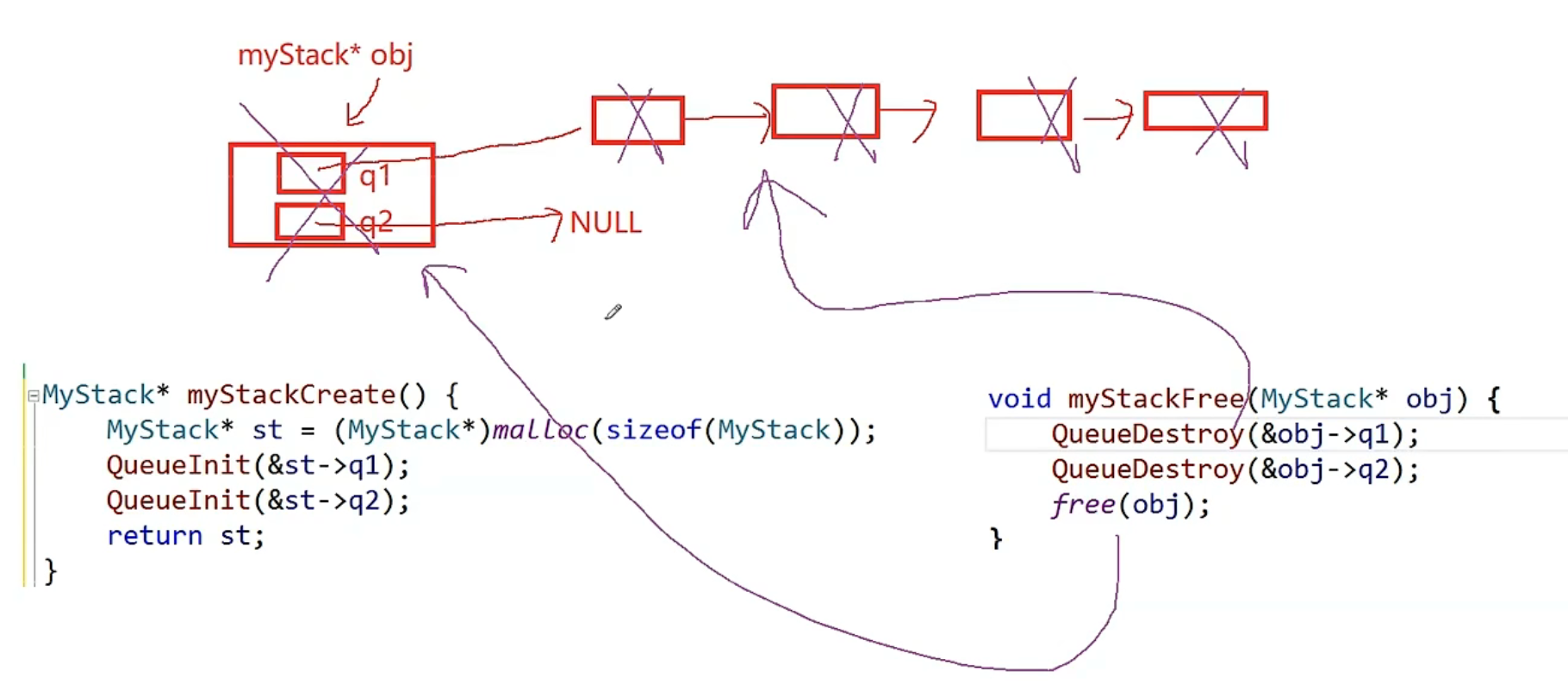
void myStackFree(MyStack* obj)
{
    //分成两步一步链表删除，一步shan'ch
    QueueDestory(&obj->q1);
    QueueDestory(&obj->q2);
    free(obj);
}
屏幕截图_20231113_181402

用栈实现队列

  • void push(int x)将元素x推到队的队尾
  • int pop( )从队列的开头移除并返回元素
  • int peak( )返回队列开头的元素
  • boolean empty( )如果队列为空，返回true，否则false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//出数据：把栈1的数据放到栈2，再由栈2出（栈2有数据就直接出，没数据就让栈1导入）    入数据：直接在栈1入
void myQueuePush(MyQueue* obj,int x)
{
    StackPush(&obj->pushST,x)//pushST指的是出数据的栈
}



int myQueuePop(MyQueue* obj)
    //如果popST中没有数据，将pushST的数据导过去
    //popST中的数据就符合先进先出的顺序了
{
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->push))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
        
    }
    int front=StackTop(&obj->popST);
    StackPop(&obj->popST);
    return front;
}


int myQueuePeek(MyQueue* obj)
{
    //如果popST中没有数据，将pushST的数据导过去
    //popST中的数据就符合先进先出的顺序了
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->push))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }
    //Peek和Pop的区别是不需要删只需要找队头数据
    return StackTop(&obj->popST);
}


bool myQueueEmpty(MyQueue* obj)
{
    //两个栈都为空才为空
    return StackEmpty(&obj->pushST) && StackEmpty(&obj->popST);
}

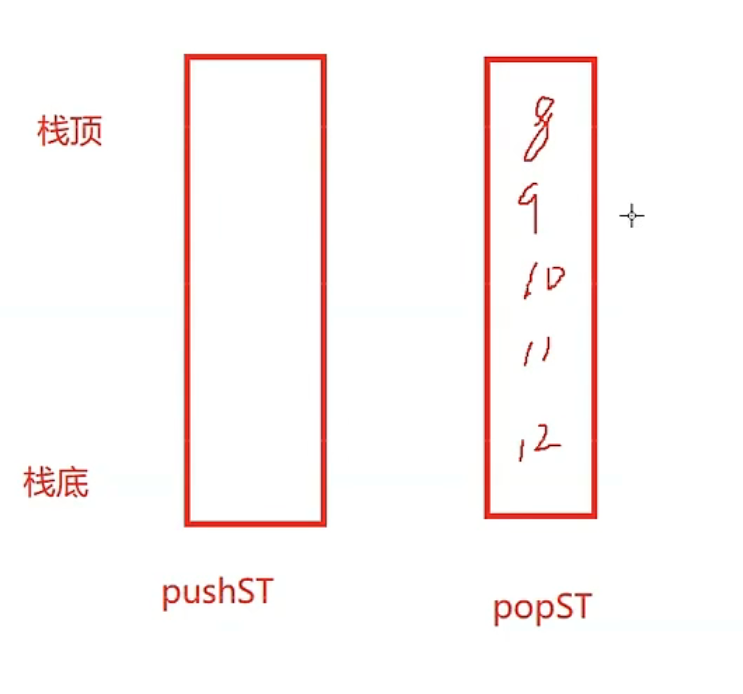
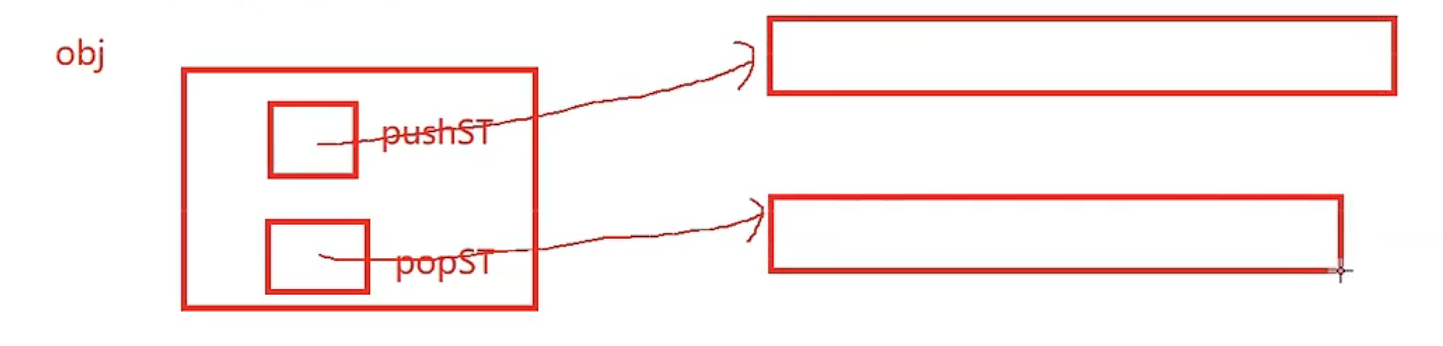
上图为逻辑图，下图为结构图（obj和两个栈，popST和pushST的关系）
屏幕截图_20231114_192143

循环队列

  • MyCircleQueue(k)：构造器，设置队列长度为k
  • Front:从对首取元素，如果队列为空，返回-1
  • Rear:获取队尾元素，如果队列为空，返回-1
  • enQueue(value):向循环队列插入一个元素，如果成功插入返回true
  • deQueue( ):从循环队列中删除一个元素，如果成功返回真
  • isEmpty( ):检查循环队列是否为空
  • isFull( ):检查队列是否已满
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/*
  符合先进先出，队列空间大小是固定的，出数据也不删除节点
  tail和front这两个指针指向同一节点则队列为空
  在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间，但是使用循环队列，我们可以用这些空间去存储新的值
  删除节点front向前移动，插入节点tail向前移动
  循环队列可以用数组实现也可以用循环链表实现。
*/
//数组
typedef struct
{
    int* a;
    int front;
    int tail;
    int k;//k指存的数据个数，k+1指空间大小
}MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k)
{
    MyCircularQueue* cq=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cq->a=(int*)malloc(sizeof(int)*(k+1));
    cq->front=cq->tail=0;
    cq->k=k;
    
    return cq;
}

bool MyCircularQueueIsEmpty(CircularQueue* obj)
{
    return obj->front==obj->tail;
}

bool MyCircularQueueIsFull(CircularQueue* obj)
{
    return (obj->tail+1)%(obj->k+1)==obj->front;
}

//入数据
bool MyCircularQueueEnQueue(CircularQueue* obj,int value)
{
    if(MyCircularQueueIsFull(obj))
        return false;
    //一定注意超出数组空间就将循环
    obj->a[obj->tail]=value;
    ++obj->tail;
    obj->tail %= (k+1);
}

//出数据
bool MyCircularQueueDeQueue()
{
    if(MyCircularQueueIsEmpty(obj))
        return false;
    ++obj->front;
    obj->front %= (k+1);
    return ture;
}

int MyCircularQueueFront(MyCircularQueue* obj)
{
    if(myCircularQueueIsEmpty(obj))
        return -1;
    
    return obj->a[onj->front];
}

int MyCircularQueueRear(MyCircularQueue* obj)
{
    if(myCircularQueueIsEmpty(obj))
        return -1;
    
    if(obj->tail == 0)
        return obj->a[k];
    else
        return a[obj->tail-1];
}

重点：循环队列，无论使用数组实现还是循环链表实现，都要多开一个空间，也就意味着要是一个存k个数据的循环队列，要开k+1个空间，否则无法实现判空和判满，避开空和满是相同的情况