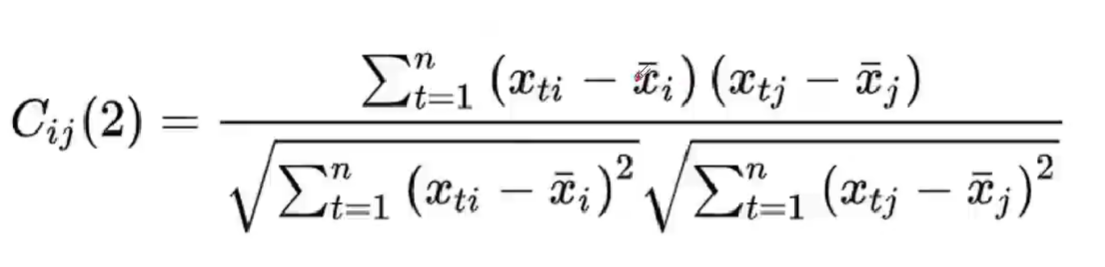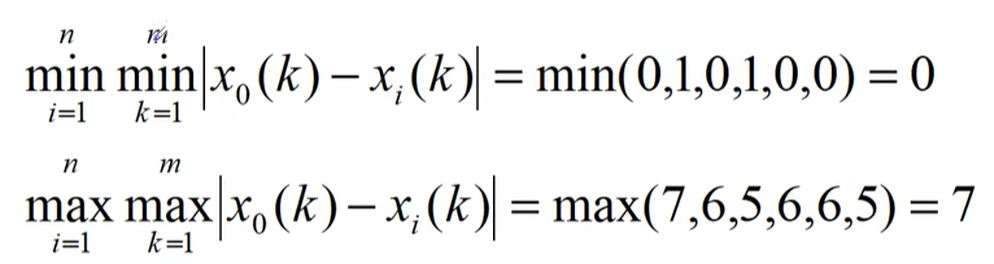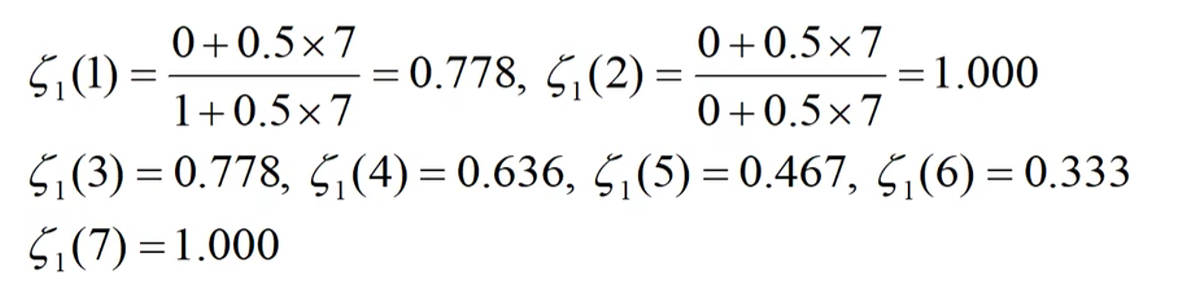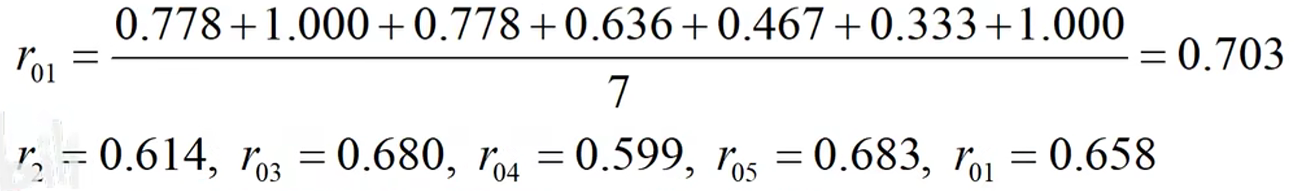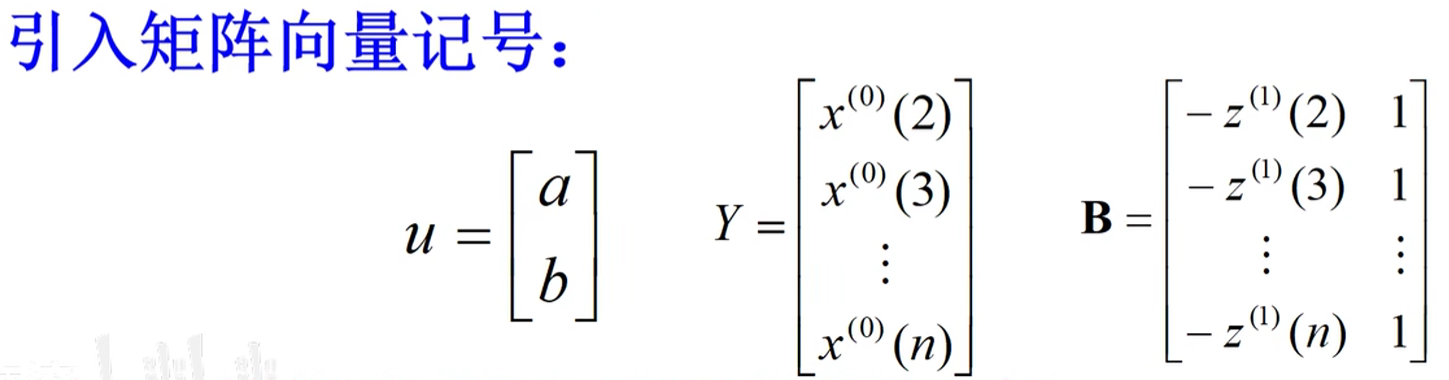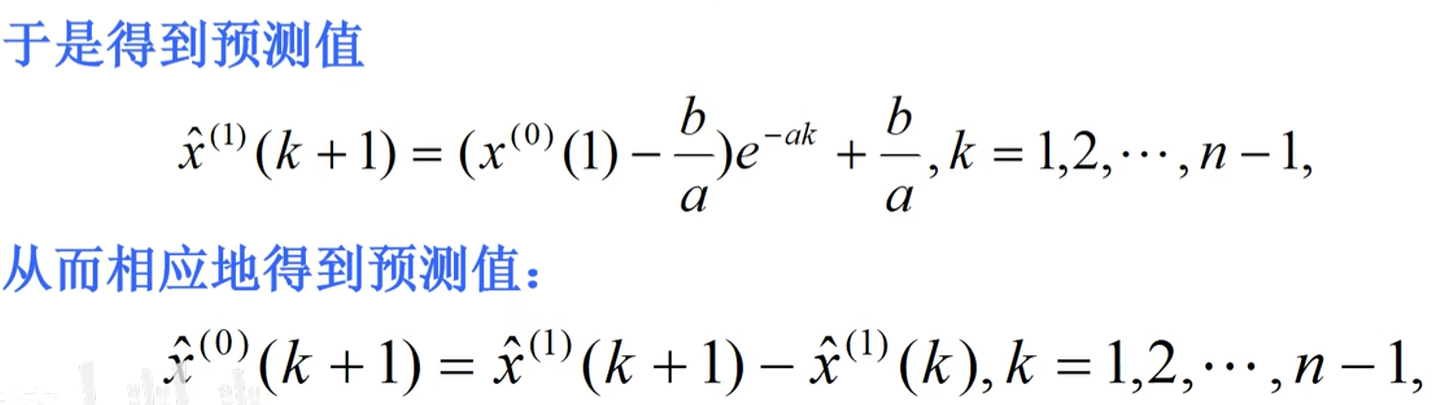数学建模算法入门(2)

TOPSIS算法

评价方法大体可以分为两类，其主要区别在确定权重的方法上。一类是主观赋权法，如综合指数法，模糊综合评判法，层次分析法，功效系数法等。另一类是客观赋权，根据各项指标间相关关系或各指标值变异程度确定权数，如主成分分析法，因子分析法，理想解法(也称TOPSIS法)

topsis:构造评价问题的正理想解和负理想解方法：设多属性决策方案集(待评价方案集)为D={d_1,d_2,…,d_m}衡量方案优劣的属性变量为x_1,x_2,…x_n这时方案集D中的每个方案d_i(i=1,…,m)的n个属性值构造的向量是[a_i1,…,a_in],它作为n维空间中的一个点，能唯一地表征方案d_i。

算法步骤：

• 消除量纲问题：用向量规划的方法求得规范决策矩阵，设多属性决策问题的决策矩阵$A=(a{ij}){m×n}$，规范化决策矩阵$B=(b{ij}){m×n}$，其中$b{ij}=a{ij}/\sqrt{\sum{i=1}^{m}{a{ij}^{2}}}$,i=1,2,…,m;j=1,2,…,n。

• 权重问题：由决策人给定各属性的权重向量为$w=[w1,w_2,…,w_n]$,则$c{ij}=wj·b{ij},i=1,2,…,m;j=1,2,…,n$属性的权重值乘以每一个数据值就是最终的评价值

• 确定正理想解$C^$和负理想解$C^0$，设正理想解的第j个属性值为$C_j^$,负理想解第j个属性值为$C_j^0$

  $$正理想解: C_j^*=\left \{ \begin{array}{lr**} max\quad c_{ij},j为效益性属性\\ min\quad c_{ij},j为成本型属性,j=1,2,...,n \end{array} \right.\\ 负理想解: C_j^0=\left \{ \begin{array}{lr**} max\quad c_{ij},j为成本性属性\\ min\quad c_{ij},j为效益性属性,j=1,2,...,n \end{array} \right.\\$$

• 计算各方案到正理想解与负理想解的距离

  $$备选方案d_i到正理想解的距离为\\ s_i^n=\sqrt{\sum_{j=1}^{n}{(c_{ij}-c_j^*)^2}},i=1,2,...,m\\ 备选方案d_i到负理想解的距离为\\ s_i^n=\sqrt{\sum_{j=1}^{n}{(c_{ij}-c_j^0)^2}},i=1,2,...,m\\$$

• 计算各方案的排队指标值$f_i^=s_i^0/s_i^+s_i^0$越大越好

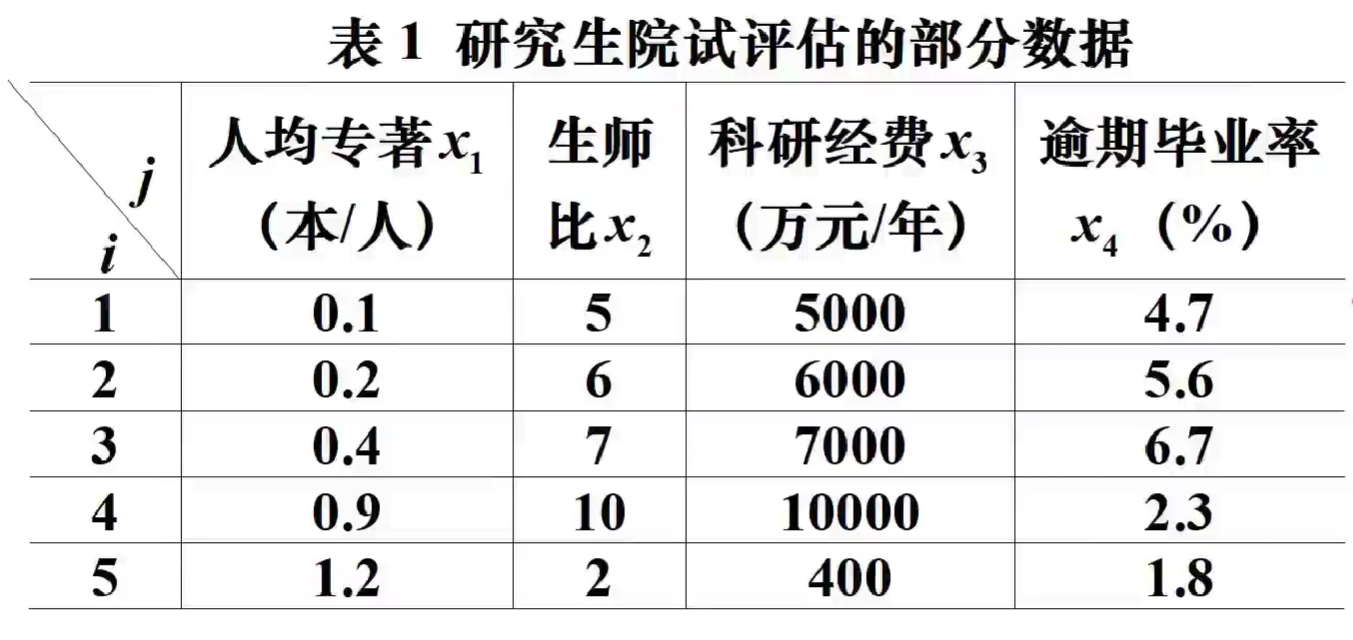
例题1.1为了客观地评价我国研究生教育的实际状况和各研究院的教学质量，国务院学位委员会办公室组织过依次研究生院的评估

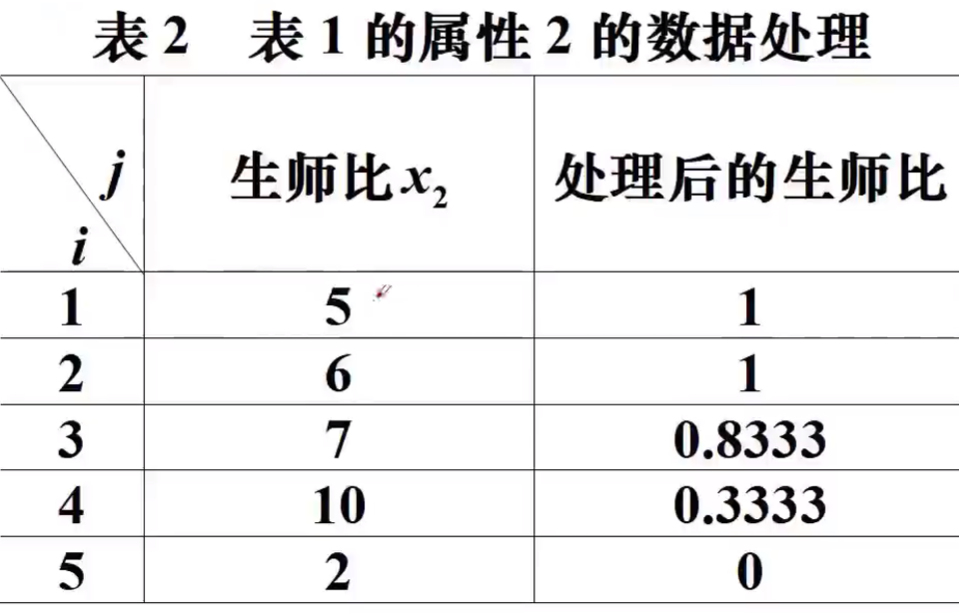
第一步：属性值的规范化—->标准的0-1变换(为了使每个属性变换后的最优值为1且最差值为0)——>全变成效益型

• 对效益性属性

  $$b_{ij}=\frac{a_{ij}-a_j^{max}}{a_j^{max}-a_j^{min}}$$

• 对成本型属性

  $$b_{ij}=\frac{a_j^{max}-a_{ij}}{a_j^{max}-a_j^{min}}$$

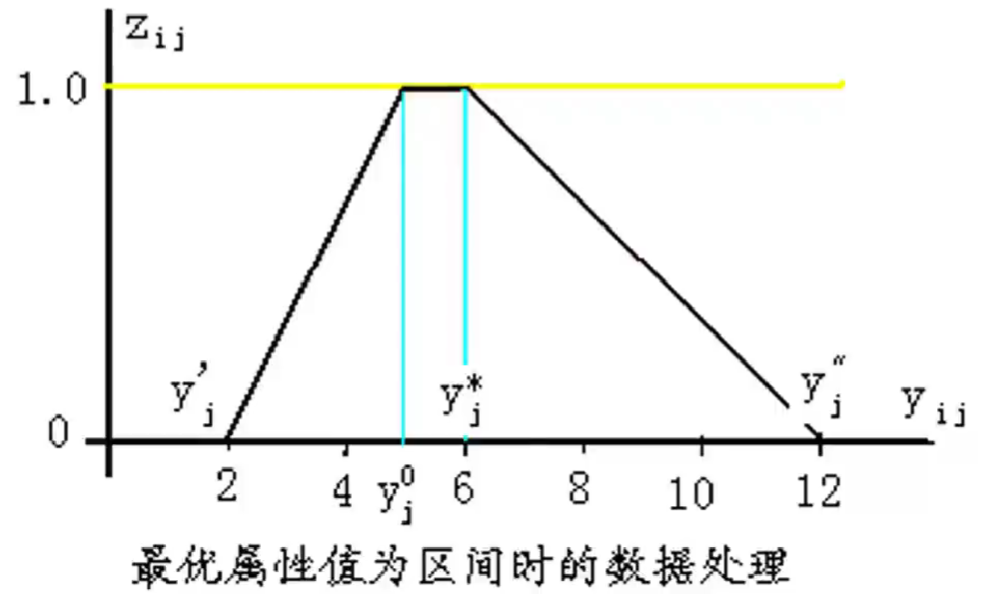
• 对于区间型，设定最优属性区间为$[a_j^0,a_j^*],a_j^{‘’}为无法容忍上限,a_j^{‘}为无法容忍下限$

$$b_{ij}=\left \{ \begin{array}{lr**} 1-(a_j^0-a_{ij})/(a_j^0-a_j^{'}),若a_j^{'}\leq a_{ij}\leq a_j^0\\ 1,若a_j^0\leq a_{ij}\leq a_j^*\\ 1-(a_{ij}-a_j^*)/(a_j^{''}-a_j^*),若a_j^*\leq a_{ij}\leq a_j^{''}\\ 0,其它 \end{array} \right.\\$$

clc，clear
%@是用于定义函数句柄的操作符。函数句柄既是一种变量，可以用于传参和赋值；也可以当作函数名一样使用
x_2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb).*(x>=lb&x<qujian(1))+...
(x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...
(x>qujian(2)&x<=ub);
qujian=[5,6];lb=2;ub=12;
x2data=[5 6 7 10 2];
y2=x2(qujian,lb,ub,x2data)

注意：这里其实是两种方法1.可以先都变成效益型的然后用向量规划的那个式子算2.之间用向量规划算，但是成本型的要将算出 来的b_ij变成1-b_ij。前提是没有区间型，要是有区间型就要先把区间型变成效益型。

聚类分析

• R型聚类作用：降维处理，将原来的变量变为某一个或某几个变量
• Q型聚类作用：分类及分析(常用)

样品间的相似度量——距离

1. 欧式距离 pdist(x)

   $$d(x_i,x_j)=|\sum_{k=I}^{P}{(x_{ik}-x{jk})^2}|^{I/2}$$

2. 绝对距离 pdist(x,’cityblock’) (几乎不用)

   $$d(x_i,x_j)=\sum_{(k=I)}^{p}{|x_{ik}-x_{jk}|}$$

3. 明氏距离 pdist(x,’minkowski’,m)

   $$d(x_i,x_j)=[\sum_{k=I}^{P}|x_{ik}-x_{jk}|^m]^{I/m}$$

4. 切氏距离 max(abs(xi-xj))

   $$d(x_i,x_j)=max_{(I\leq k\leq p)}{|x_{ik}-x_{jk}|}$$

5. 方差加权距离，将原数据标准化以后的欧式距离

   $$d(x_i,x_j)=[\sum_{k=I}^{p}{(x_{ik}-x_{jk})}^2/s_k^2]^{I/2}$$

6. 马氏距离 pdist(x,'mahal')

   $$d(x_i,x_j)=\sqrt{(x_i-x_j)^T\Sigma_{-1}(x_i-x_j)}式子中\Sigma_{-1}为向量x和y的协方差矩阵的逆矩阵$$

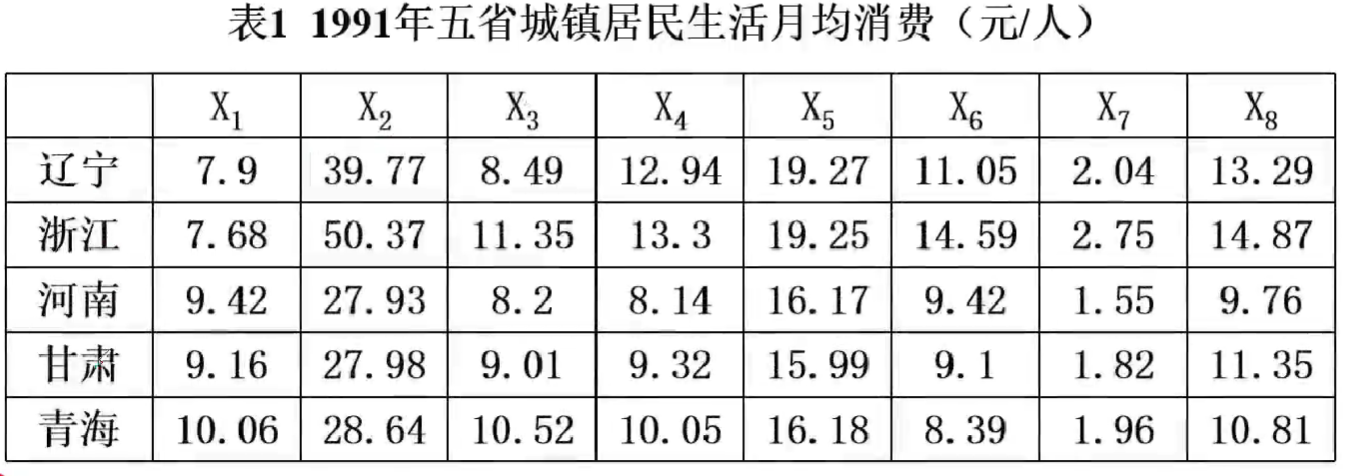
例题1.1为了研究辽宁，浙江，河南，甘肃，青海五省1991年城镇居民生活消费规律，需要利用调查资料对五个省进行分类，指标变量共8个，意义如下：x1：人均粮食支出，x2：人均副食支出，x3：人均烟酒茶叶支出，x4：人均其他副食支出，x5：人均衣着商品支出，x6：人均日用品支出，x7：人均燃料支出，x8：人均非商品支出

d1=pdist(a)%此时计算出各行之间的欧式距离,为了得到书中的距离矩阵，我们输入命令
D=squareform(d1)%注意此时d1必须是一个行向量，结果是实对称矩阵
S=tril(squareform(d1))%若想要得到三角阵

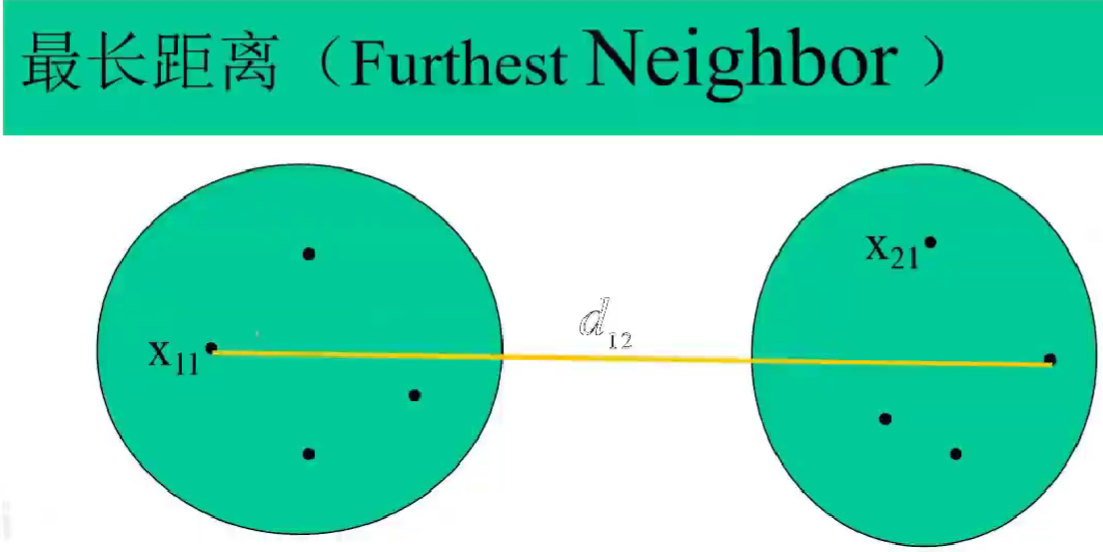
类间距离

d_ij表示两个样品x_i,x_j之间的距离，G_p,G_q分别表示两个类别，各自含有n_p,n_q个样品

• 最短距离 :即用两类中样品之间的距离最短者作为两类间的距离

• 最长距离：即用两类中样品之间的距离最长者作为两类间的距离

• 类平均距离：即用两类中所有两两样品之间距离的平均作为两类间距离

• 重心距离：两类的重心之间的欧式距离作为两类的距离

常见聚类方法的步骤

谱系聚类法

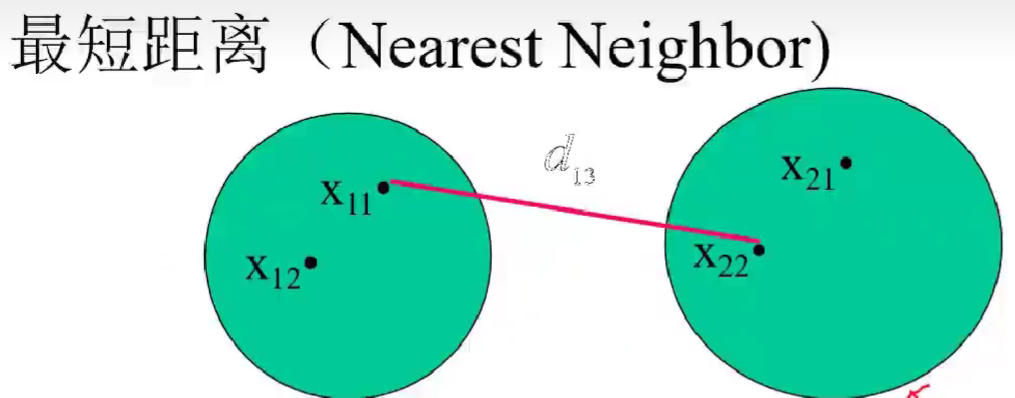
1.选择样本间距离的定义(一般为欧氏距离)及类间距离的定义(一般为最短距离)

2.计算n个样本两两间的距离，得到距离矩阵D=(d_ij)

3.构造个类，每类只含有一个样本

4.合并符合类间距离定义要求的两个类作为一个新类

5.计算新类与当前各类的距离。若类的个数为1，则转到步骤6，否则回到步骤4

6.画出聚类图

7.决定类的个数和类

例题1.1.2为了研究辽宁等5省1991年成长居民生活消费情况的分布规律，根据调查资料做类型分类，用最短距离做类间分类，数据如表1

将每个省视为一个样品，先计算5个省区之间的欧氏距离，用D0表示距离矩阵(前一问已经构建出来)，可得：

     (1)   (2)   (3)   (4)   (5)
(1)   0
(2) 11.67   0
(3) 13.80 24.63   0
(4) 13.12 24.06  2.20    0
(5) 12.80 23.54  3.51   2.21   0

D0(3,4)=2.20最小因此要把3，4合并为一类,为类6，代替了3，4两类。

类6与剩余的1，2，5之间的距离分别为：

d(3,4)_1=min(d31,d41)=min(13.80,13.12)=13.12

d(3,4)_2=min(d32,d42)=min(24.63,24.06)=24.06

d(3,4)_5=min(3.51,2.21)=min(3.51,2.21)=2.21

得到一个新矩阵：

D1：
       G6     G1    G2    G5
G6      0
G1    13.12    0
G2    24.06  11.67   0
G5    2.21   12.80  23.54  0

D1(6,5)=2.21最小因此要把6，5合并成一类，为类7，代替了6，5两类

类7与剩余的1，2之间的距离分别为:

d(5,6)_1=min(d51,d61)=min(12.80,13.12)=12.80

d(5,6)_2=min(d52,d62)=min(23.54,24.06)=23.54

再得到一个新矩阵：

D2:
      G7     G1     G2
G7    0
G1   12.80    0
G2   23.54  11.67    0

D2(1,2)=11.67最小因此要把1，2合并成一类，为类8，代替了1，2两类

此时，我们有两个不同的类，类7和类8，它们的距离

d(7,8)=min(d71,d72)=min(12.80,23.54)=12.80

最后得到新矩阵：

       G7     G8
G7      0
G8    12.80   0

最后合并成一个大类。

%谱系聚类的MATLAB实现
%1.输入数据矩阵，注意行与列的实际意义
%2.计算各样品之间的距离，这里用的是欧式
d=pdist(A);%欧式距离
%以上命令输出结果是一个行向量，如果要得到距离矩阵，可以用命令
D=squareform(d);
%三角阵的命令为
D=tril(squareform(d1))%下三角函数
%选择不同的类间距离进行聚类，这里用的是最短距离
z1=linkage(d);%不仅把最短距离做出了了，而且把分类结果也做出来了
%作出谱系聚类图
H=cluster(z,k)%k是分类数目，z是最短距离的结果
Find(T==k0)%找出属于第k0类的样品编号
%输出分类结果
T=cluster(z1,3)%结果表明，若分为3类，辽宁是一类，浙江是一类，河南，甘肃，青海是一类

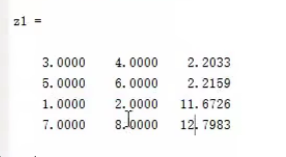
以下为z1=linkage(d)的聚类结果

K-平均聚类法

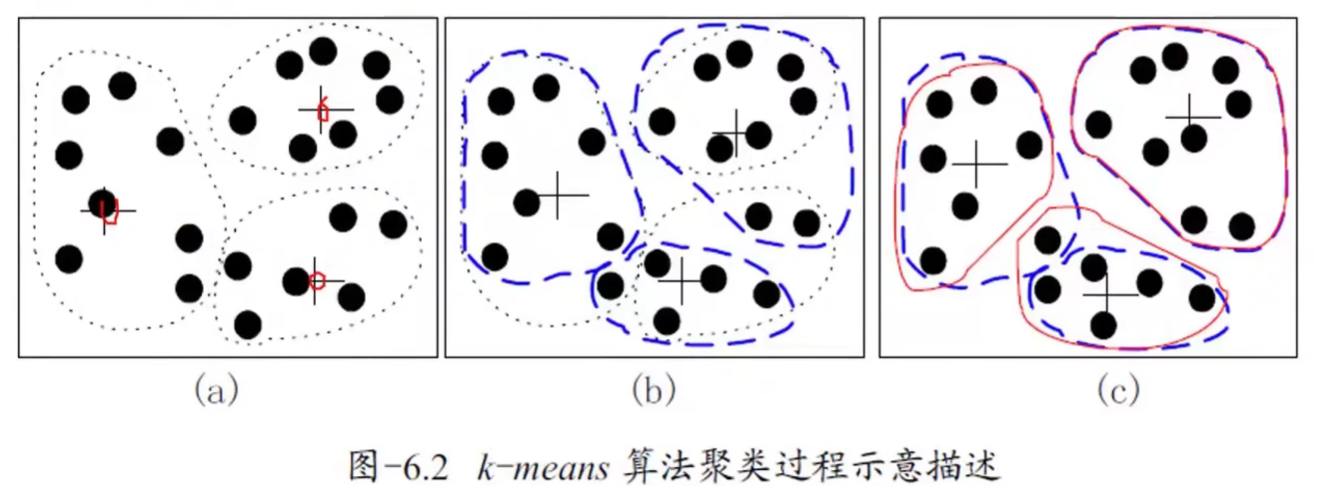
1. 从n个数据对象任意选择k个对象作为初始聚类中心
2. 循环3和4直到每个聚类不再发生变化为止
3. 根据每个聚类对象的均值(中心对象)，计算每个对象与这些中心对象的距离，并根据最小距离重新对相应对象进行分析（第一次中心对象是指定的，之后中心对象是分配到每个类的对象的平均值，进行不断的更新中心对象）
4. 重新计算每个(有变化)聚类的均值(中心对象)

注意:只适应于聚类均值有意义的场合，当数据集中包含符号属性时，直接应用k-means算法就有问题；用户必须事先指定k的个数；对噪声和孤立点数敏感，少量的该类数据能够对聚类均值起到很大影响；刚开始取中心对象可以不是样本点

例题1.2假设空间数据对象分布如图(a)所示，设k=3，也就是需要将数据集划分为三份(聚类)

clear all
clc
x=[0  1  0  1  2  1  2  3  6  7  8  6  7  8  9  7  8  9  0  9;0  0  1  1  1  2  2  2  6  6  6  7  7  7  7  0  0  9  9];
figure(1)
plot(x(1,:),x(2,:),'r*')%横轴为第一行所有列，纵轴为第二行所有列，红色星号表示
%%第一步选取聚类中心，即令K=2
z1=[x(1,1);x(2,1)];
z2=[x(1,2);x(2,2)];%聚类中心为z1(0,0) z2(0,1)
R1=[];
R2=[];%分成两个聚类，用于储存成员
t=1
K=1;%记录迭代的次数
dif1=inf;%inf为正无穷
dif2=inf;
%%第二步计算各点与聚类中心的距离
%(inf表示最大值，eps表示最小值)只要两次聚类中心不等构成无限循环
while(dif1>eps&dif2>eps)
for i=1:20
dist1=sqrt((x(1,i)-Z1(1)).^2+(x(2,i)-Z1(2)).^2);
dist2=sqrt((x(1,i)-Z2(1)).^+(x(2,i)-Z2(2)).^2);
temp=[x(1,i),x(2,i)]';
if dist1<dist2
R1=[R1,temp];
else
R2=[R2,temp];
end
end
Z11=mean(R1,2);%mean(A,2)包含每一行的平均值的列向量(对行求平均值)
Z22=mean(R2,2);%得到新的聚类中心
t1=z1-z11;%%测试两次是不是相等，可以有多种方法这里只简单的列举一种
t2=z2-z22;
dif1=sqrt(dot(t1,t1));%dot两个向量的点积
dif2=sqrt(dot(t2,t2));
Z1=z11;
Z2=z22;
K=K+1;
R1=[];
R2=[];
end
hold on
plot([Z1(1),Z2(1)],[Z2(2),Z2(2)],'g+')%最终得到的聚类中心用绿色加号

变量间的相似度量——相似系数

当对p个指标变量进行聚类时，用相似系数来衡量变量之间的相似程度(关联度)，若用 $C_{\alpha \beta}$表示变量之间的相似系数，则应满足

$$|C_{\alpha\beta}|\leq1且C_{\alpha\alpha}=1\\ C_{\alpha\beta}=\pm1,当且仅当\alpha=k\beta,k\neq0\\ C_{\alpha\beta}=C_{\beta\alpha}$$

两个变量完全相似(一个变量由另一个变量乘以一个整数得到)，此时相似系数为1

相似系数中最常用的是相关系数与夹角余弦

• 两变量的夹角余弦定义为

$$C_{ij}(1)=\cos\alpha_{ij}=\frac{\sum_{(t=1)}^{n}{x_{ti}x_{tj}}}{\sqrt{\sum_{t=1}^{n}{x_{ti}^{n}}}\sqrt{\sum_{t=1}^{n}{x_{tj}^2}}}$$

• 两变量的相关系数定义

计算例题1中各指标之间的相关系数与夹角余弦

a=[7.9   39.77  8.49  12.94 19.27 11.05 2.04 13.29
   7.68  50.37  11.35 13.3  19.25 14.59 2.75 14.87
   9.42  27.93  8.2   8.14  16.17 9.42  1.55 9.76
   9.16  27.98  9.01  9.32  15.99 9.1   1.82 11.35
   10.06 28.64  10.52 10.05 16.18 8.39  1.96 10.81]
R=corrcoef(a);%指标之间的相关系数
a1=normc(a);%将a的各列化为单位向量
J=a1'*a1%计算a中各列之间的夹角余弦

GM(1,1)灰色预测

灰色预测法用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征值，或达到某一特征量的时间

灰色预测的四种常见类型

• 灰色时间序列预测：即用观察到的反映预测对象特征的时间序列来构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间
• 畸变预测：即通过灰色模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内(异常气候，预测零件问题时间)
• 系统预测：通过对系统行为特征指标建立一组相互关联的灰色预测模型，预测系统中众多变量之间的相互协调关系的变化(用的次数比较少)
• 拓扑预测：将原始数据做曲线，在曲线上按定值寻找该定值发生的所有时点，并以该定值为框架构成时点数列，然后建立模型预测该定值所发生的时点

灰色关联度:

$\zeta_i(k)=\frac{min_imin_k|X_0(k)-X_i(k)|+\rho max_imax_k|X_0(k)-X_i(k)|}{|X_0(k)-X_i(k)|+\rho max_imax_k|X_0(k)-X_i(k)|}$

$X_0(k)表示标准数列中的第k个元素，例如：x_0(1)为标准列中的第一个元素\假设有m个比较数列X_i(k)表示第i个数列中的第k个元素(i=1,2,…,m),\rho一般取0.5$

$上述式子中min_imin_k|X_0(k)-X_i(k)|表示先找出每个比较数列中的每个元素和标准数列中每个元素差值的最小值再找出这些元素中的最小值$

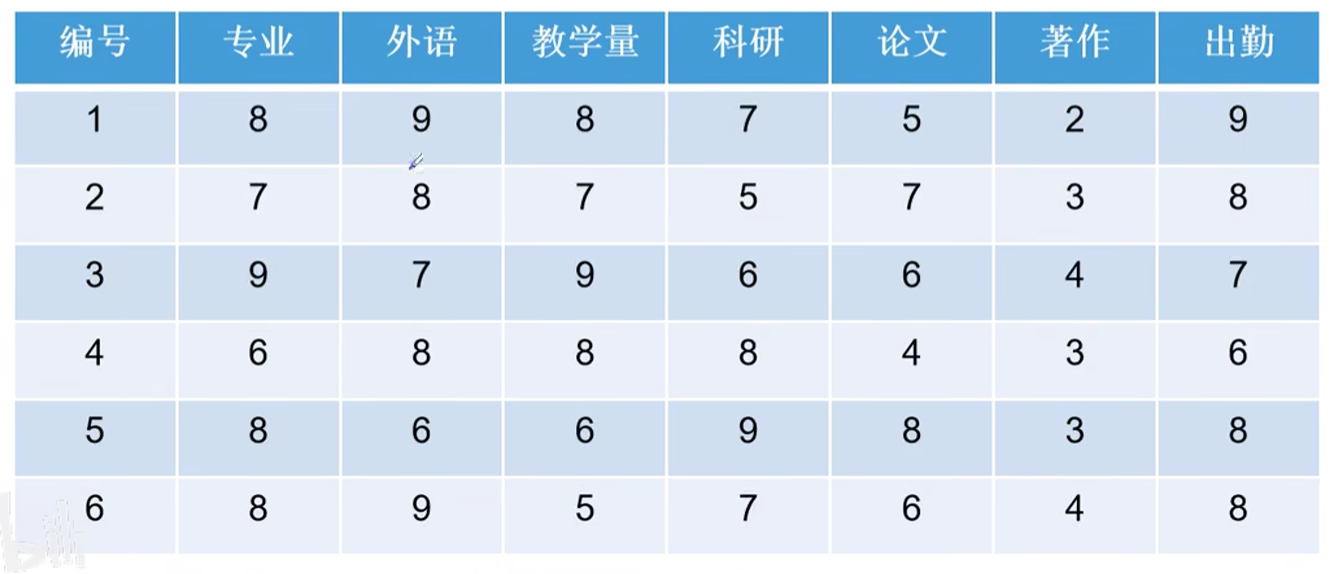
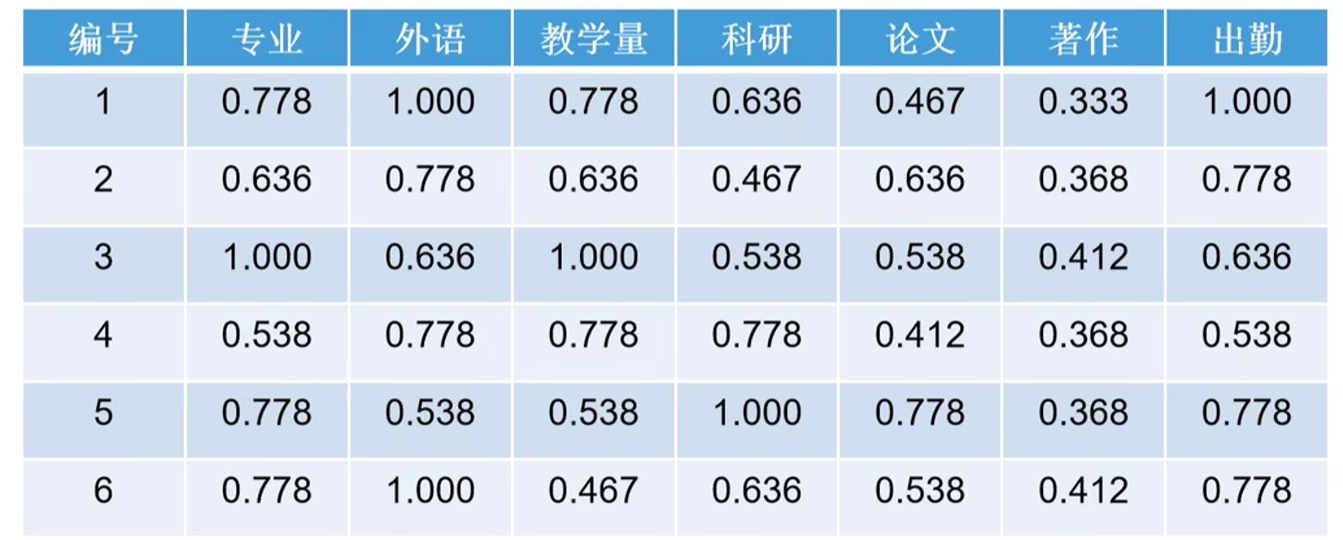
例题利用灰色关联分析对6位教师工作状况进行综合分析

1.确定参考数列{x_0}={9 9 9 9 8 9 9}

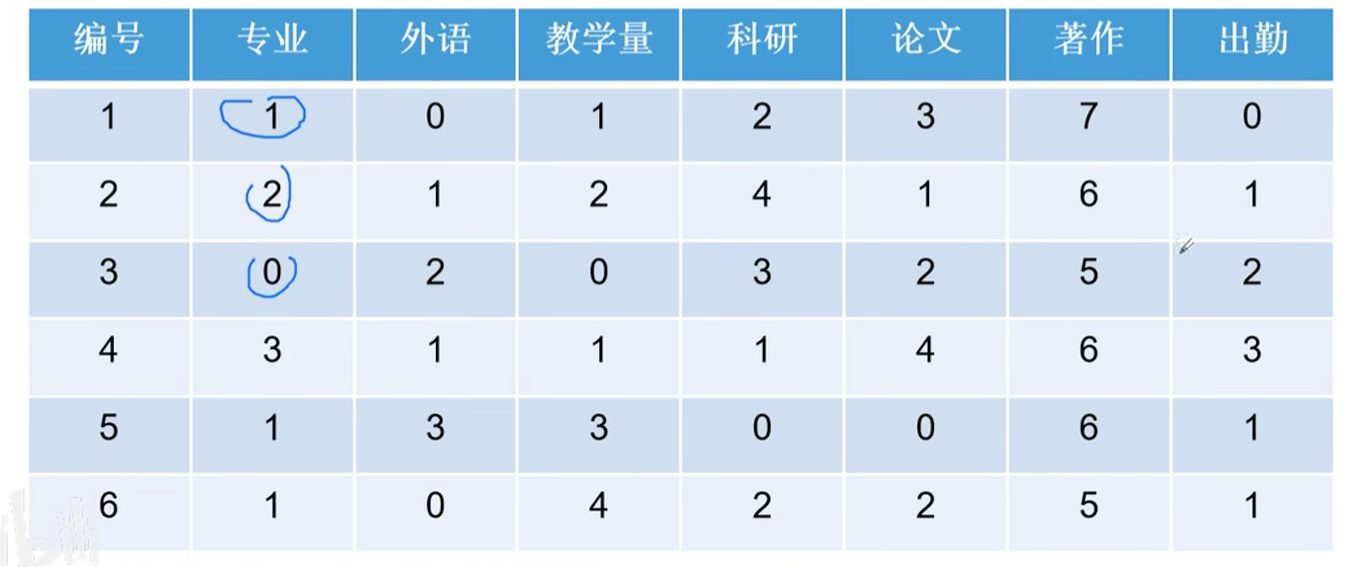
2.计算$|x_0(k)-x_j(k)|$见下表

3.求最值

4.带入上述公式得

注意：这里给出的只有第一个老师的数据还要求$\zeta_2(k),\zeta_3(k)…,\zeta_6(k)其中k=1,2,…,7$结果如下

5.分别计算每个人各指标关联系数的均值(关联序)：

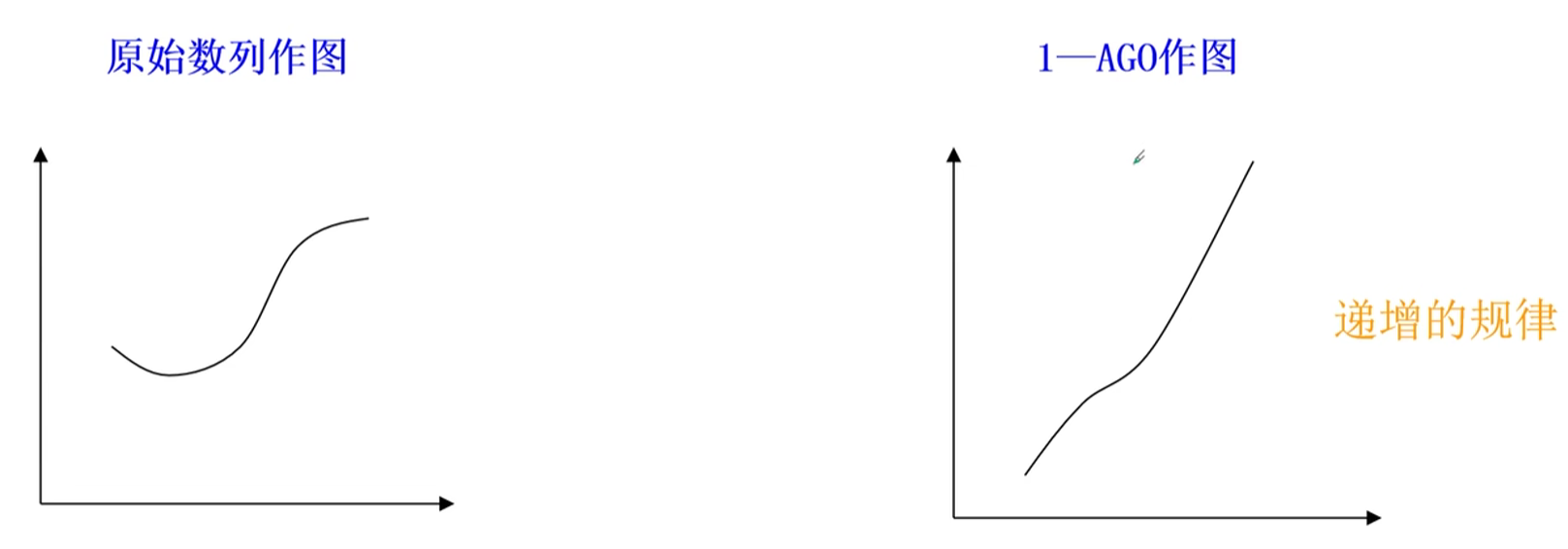
灰色生成数列：一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。数据生成的常用方式有累加生成,累减生成，和加权累加生成

• 累加生成(AGO)：把数列各项(时刻)数据依次累加的过程称为累加生成过程

  $$x^{(1)}{(k)}=\sum_{i=1}^{k}{x^{(0)}(i)},k=1,2,...,n\\ 称所得到的新数列为数列x^{(0)}的一次累加数列，类似的有\\ x^{(r)}{(k)}=\sum_{i=1}^{k}{x^{(r-1)}(i)},k=1,2,...,n,r\geq1\\称为原始数列x^{(0)}的第r次累加数列\\ 例:x^{(0)}=[1,2,3,4 ...],则经过累加后x^{(1)}=[1,3,6,10...]$$

• 累减生成(IAGO):对于原始数据列依次做前后相邻的两个数据相减的运算过程称为累减生成过程

$$如果原始数列为:x^{(1)}=(x^{(1)}(1),x^{(1)}(2),x^{(1)}(3)...,x^{(1)}(n))\\ 令x^{(0)}{k}=x^{(1)}{(k)}-x^{(1)}{(k-1)},k=2,3,...,n\\累减(或累加)后的数列第一个数为原始数据第一个数\\ 例如:x^{(1)}=[1,2,3,4],经过累减后x^{(0)}=[1,1,1,1]$$

注意:从这里的记号可以看到，从原始数列x(0)得到新数列x(1)，在通过累减生成可以还原出原始序列。$实际运用在数列x^{(1)}的基础上预测出x^{(<1>)},通过累减生成得到预测数列x^{0}$

• 加权邻值生成

  $$设原始数列为x^{(0)}=(x^{(0)}(1),x^{(0)}(2),x^{(0)}(3),...,x^{(0)}(n))\\称x^{(0)}(k-1),x^{(0)}(k)为数列x^{(0)}的任意一对邻值，x^{(0)}(k-1)为后邻值，x^{(0)}(k)为前邻值\\ 对于常数\alpha 属于[0,1]区间内，令z^{(0)}(k)=\alpha x^{(0)}(k)+(1-\alpha)x^{(0)}(k-1),k=2,3,...,n\\ 由此得到的数列z^{(0)}称为数列x^{(0)}在权值\alpha下的邻值生成数，权\alpha也称为生成系数\\ 特别地，当生成系数\alpha=0.5时，则称z^{(0)}(k)=0.5x^{(0)}(k)+0.5x^{(0)}(k-1),k=2,3,...,n为均值生成数，也称等权邻值生成树\\ 例如x^{(0)}=[1,2,3,4],z^{(0)}=[0.5,1.5,2.5,7.5]$$

灰色生成数列的后续构建函数由微分函数构成

• 定义累加后数列x(1)的灰导数为：$d(k)=x^{(0)}{k}=x^{(1)}(k)-x^{(1)}(k-1)$

• 定义邻值生成后数列z(0)的灰导数为：$x^{(0)}{k}+az^{(1)}(k)=b,其中x^{(0)}为灰导数a为发展系数，z^{(1)}{(k)}称为白化背景值，b称为灰作用量$灰色导数方程中只有a和b两个未知量但是实际给的方程预测点很多，这样就存在多余方程和多余解——-用最小二乘法求解多余解

最小二乘得到:$u^T=(a,b)^T=(BB^T)^{-1}B^TY$

$$GM(1,1)的灰微分方程对应于的白微分方程为:\\ \frac{dx^{(1)}{(t)}}{dt}+ax^{(1)}{(t)}=b$$

GM(1,1)灰色预测的步骤

1. 数据的检验与处理

   $$设原始序列为x^{(0)}=(x^{(0)}{(1)},x^{(0)}{(2)},...,x^{(0)}{(n)})\\计算数列的级比:\\ \lambda{(k)}=\frac{x^{(0)}{(k-1)}}{x^{(0)}{(k)}},k=2,3,...,n\\ 如果所有的级比都落在可容覆盖区间X=(e^{\frac{-2}{n+1}},e^{\frac{2}{n+1}})\\ 否则对数据做适当的变换处理，如平移变换(加减一共数c):\\ y^{(0)}{(k)}=x^{(0)}{(k)}+c,k=1,2,...,n,使得符合级比检验$$

2. 构造数据矩阵B和数据向量Y

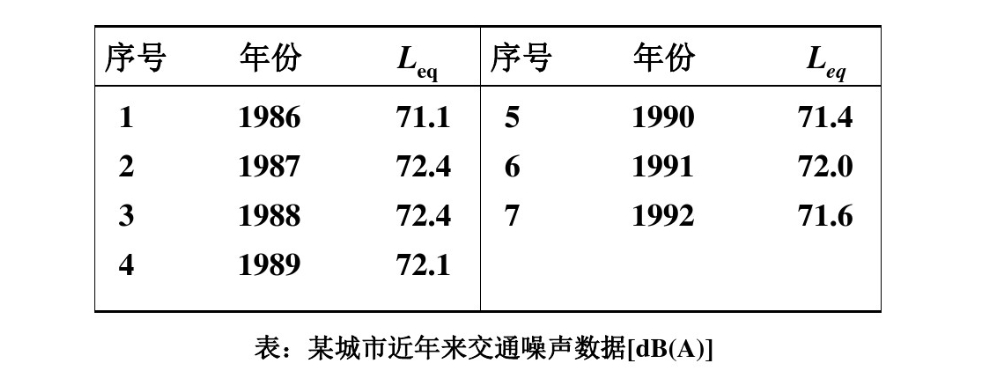
   这里用一个例题来说明：

   

   • 数据矩阵B的构造方法：

     • 对原始序列做一次累加：

       $$x^{(1)}{(k)}=\sum_{m=1}^{k}{x^{(0)}}{(m)},k=1,2,...,7\\ 得到:X^{(1)}=(x^{(1)}{(1)},x^{(1)}{(2)},...,x^{(1)}{(7)})={71.1,143.5,215.9,288,359.4,431.4,503}$$

     • 用加权临值生成：这里$\alpha=0.5,Y=\alpha(x^{(1)}(1)+x^{(1)}(2))…$

       

   最后得到:Y和B

   

3. 其中a，b用最小二乘法得到：

   $$P=(a,b)^T=(BB^T)^{-1}B^TY=\\(0.00234379\\ 72.6572696)$$

4. 建立GM(1,1)模型

   $$不妨设x^{(0)}=(x^{(0)}{(1)},x^{(0)}{(2)},...,x^{(0)}{(n)})满足级比，以它为数列建立GM(1,1)模型\\ x^{(0)}{(k)}+az^{(1)}{(k)}=b\\ 相应的白化模型为:\\ \frac{dx^{(1)}{(t)}}{dt}+ax^{(1)}{(t)}=b\\ 得到时间响应序列:x^{(1)}{(t)}=(x^{(0)}{(1)}-\frac{b}{a})e^{-a(t-1)}+\frac{b}{a}\\$$

5. 得到预测

其中x^^(1)^(1)=x^^(0)^(1)=x^(1)^(1)=71.1得到:x^^(1)^(k+1)=-30928.85259e^-0.00234379k^+30999.95259

插值与拟合基本原理

插值问题(已知函数在某区域内若干点处的值，求函数在该区间内其他点处的值)

注意因为Runge不应该使用七次以上的差值，为避免这一现象常用的方法是：将差值区间分成若干小区间，在小区间内用低次差值

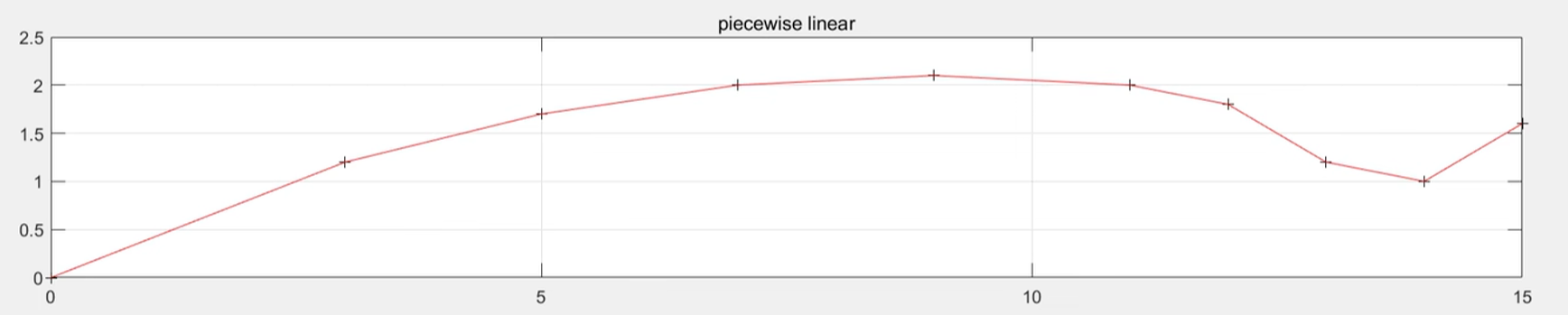
例题1.1在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为12，9，9，10，18，24，28，27，25，20，18，15，13推测中午1点温度，并作出24小时温度变化曲线图

matlab差值

• 一维插值命令是interp1,其基本格式是$yi=interp1(x,y,xi,’method’)$,其中x，y为已知点坐标，xi为要差值点，通常x,y,xi为向量，’method’表示插值方法：’nearest’为最邻近插值，’linear’为线性插值，’spline’为三次样条插值，’cubic’为立法插值，缺省为线性插值

x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
x1=13;
y1=interp1(x,y,x1,'spline')
xi=0:1/3600:24;%从0开始每次增加3600分之一到24
yi=interp1(x,y,xi,'spline');
plot(x,y,'*',xi,yi)

function plane
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=lagrange(x0,y0,x);%拉格朗日插值
y2=interp1(x0,y0,x);%缺省用线性插值
y3=interp1(x0,y0,x,'spline');
subplot(3,1,1);%作出三行一列的图
plot(x0,y0,'k+',x,y1,'r');%第一个图放上拉格朗日插值出的,'k+'为黑色
grid;%加上网格
title('lagrange');
subplot(3,1,2);%第二个图放的是如下内容
plot(x0,y0,'k+',x,y2,'r');
grid;
title('piecewisee linear');
subplot(3,1,3);%第三个图放的是如下内容
plot(x0,y0,'k+'x,y3,'r');%样条函数插值出来的
grid;
title('spline');
function y=lagrange(x0,y0,x)%如下是拉格朗日函数的步骤,先建立这个函数，再输入上述代码
n=length(x0);m=length(x);
for i=1:m
  z=x(i);
  s=0.0;
  for k=1:n
    p=1.0;
  for j=1:n
     if j~=k
       p=p*(z-x0(j))/(x0(k)-x0(j));
       end
    end
    s=p*y0(k)+s;
   end
  y(i)=s;
  end

• 二维插值命令是interp2，基本格式为$zi=interp2(x,y,z,xi,yi,’method’)$x,y,z为插值点，z可以理解为被插值函数在(x,y)处的值，xi,yi为被插值点，zi为输出的插值结果，可以理解为插值函数在(xi,yi)处的值，x,y为向量，xi,yi为向量或矩阵，而z和zi则为矩阵，’method’表示插值方法：’nearest’为最邻近插值，’linear’为双线性插值，’spline’为双三次样条插值，默认为线性

x=1:5;
y=1:3;%x有5个数，y有3个数，可以构建出15个点
temps=[82 81 80 82 84；79 63 61 65 81；84 84 82 85 86];
figure(1);
mesh(x,y,temps);
xi=1:0.2:5;
yi=1:0.2:3;
zi=interp2(x,y,temps,xi,yi,'cubic');
figure(2);
mesh(xi,yi,zi);%plot3为空间曲线,mesh为空间曲面网格图,surf为空间曲面表面图,contour为等高线,以上为三维图的画图
figure(3);
contour(xi,yi,zi,20,'r');%建立20条等高线，把zi相等的链接起来，等高线不会相互链接,'r'为颜色
[i,j]=find(zi==min(min(zi)));%min(zi)为这一列的最小值则min(min(zi))为所有最小值
x=xi(j),y=yi(i),zmin=zi(i,j)
[i,j]=find(zi==max(max(zi)));
x=xi(j),y=yi(i),zmax=zi(i,j)

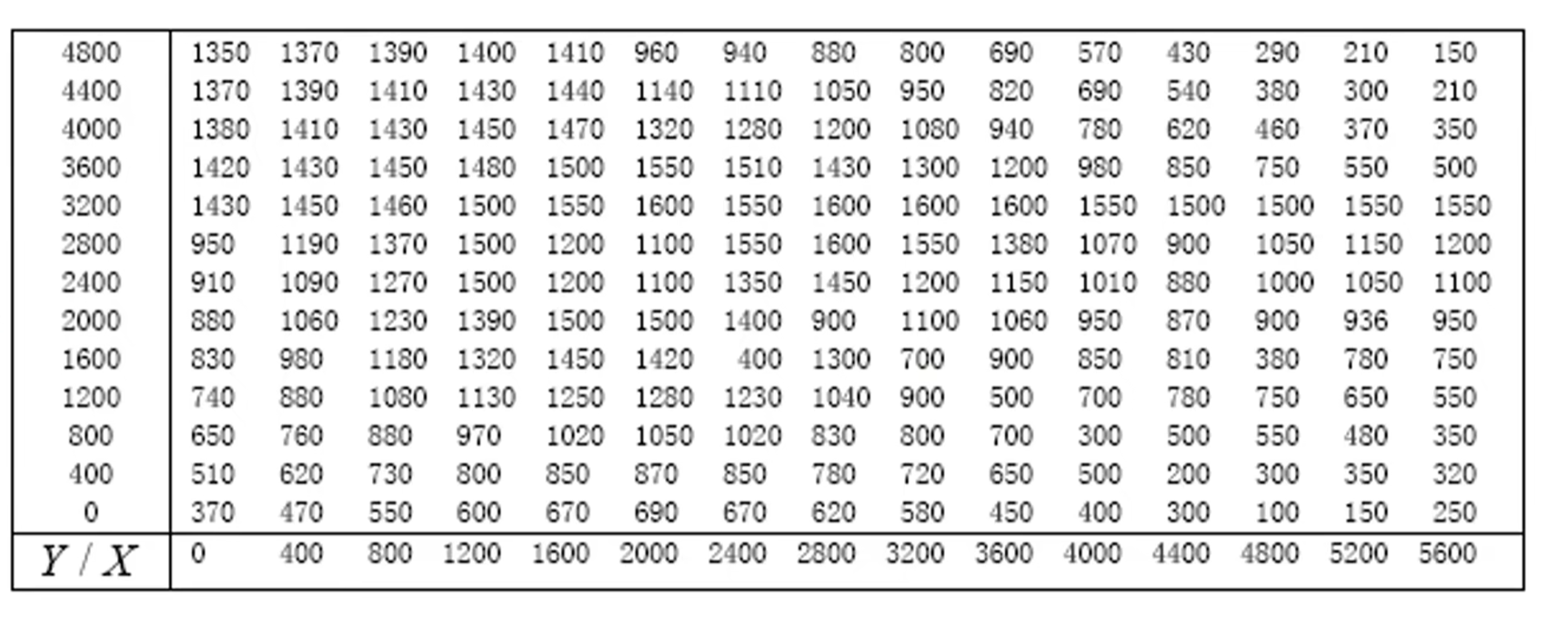
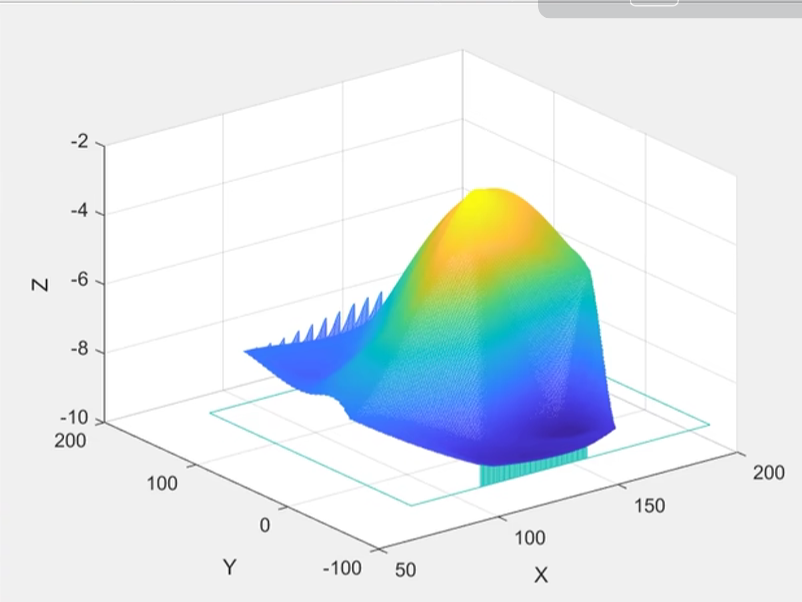
例题1.2在某山区测得一些地点的高程如下表，平面区域为0<x<5600,0<y<4800,用matlab中的最邻近邻值，双线性插值和双三次插值三种方法作出该山区的地貌图和等高线图，并求出最高点和最低点

x=0:400:5600;
y=0:400:4800;
z=[如上图];
figure(1);
meshz(x,y,z);
xlable('X'),ylable('Y'),zlable('Z');%横轴坐标的名字叫X...
[xi,yi]=meshgrid(0:50:5600,0:50:4800);
figure(2);
zli=interp2(x,y,z,xi,yi,'nearest');
surfc(xi,yi,z1i);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(3);
z2i=interp2(x,y,z,xi,yi);
surfc(xi,yi,z2i);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(4);
z3i=interp2(x,y,z,xi,yi,'cubic');
surfc(xi,yi,z3i);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(5);
subplot(1,3,1),contour(xi,yi,z1i,10,'r');
subplot(1,3,2),contour(xi,yi,z2i,10,'r');
subplot(1,3,3),contour(xi,yi,z3i,10,'r');

注意：前面讨论的插值问题的插值点(x,y)均为网格点，当(x,y)为散乱点时可用$griddata(x,y,z,xi,yi,’method’)$进行二维插值

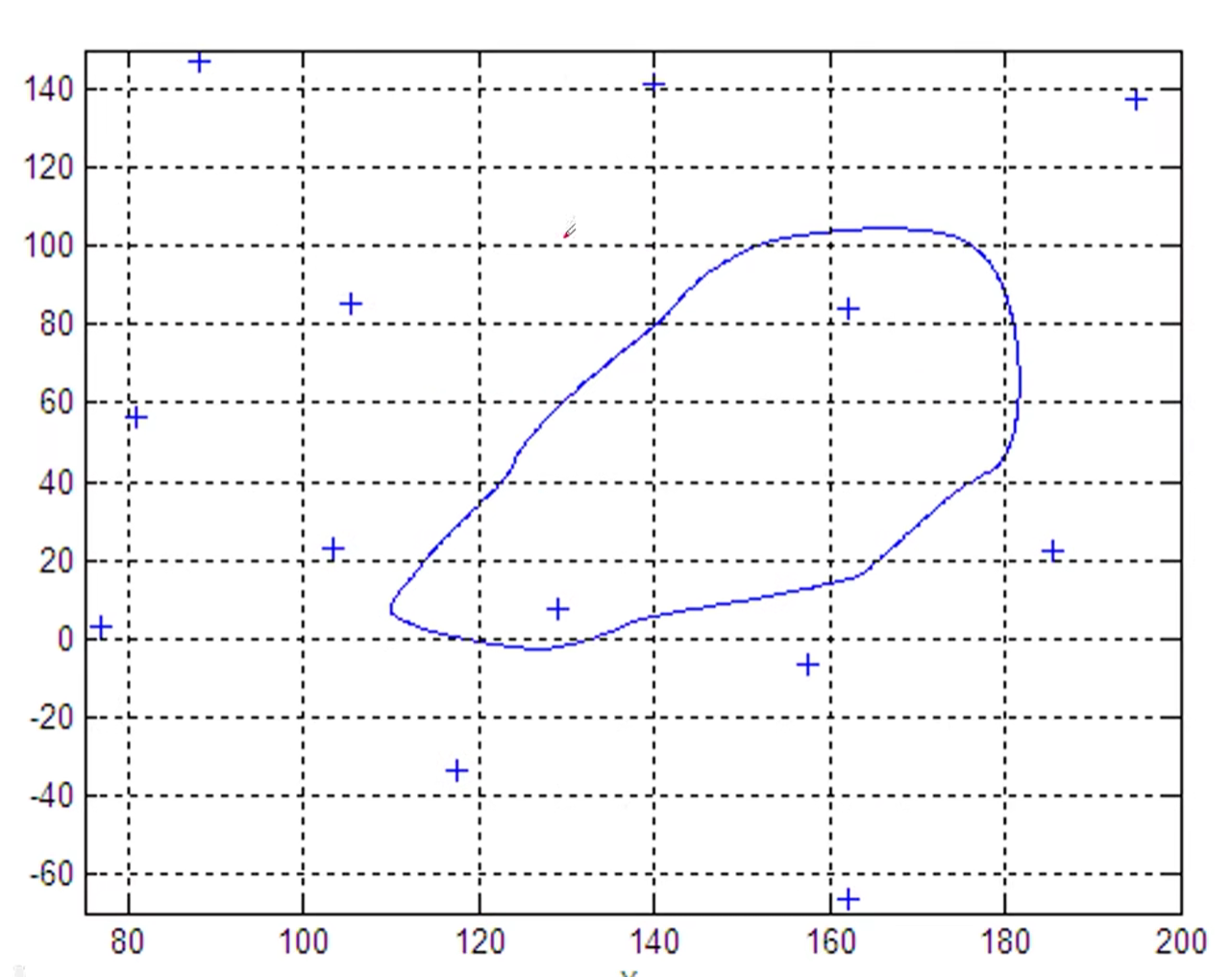
例题1.3在某海域测得一些点(x,y)处的水深如下表，船的吃水深度为5英尺，在矩形区域(75,200)*(-50,150)内的哪些地方船要避免进入

clear
x=[如上图];
y=[如上图];
z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];%先把z变成负数，再变成正数
[xi,yi]=meshgrid(75:0.5:200,-50:0.5:150);
zi=griddata(x,y,z,xi,yi,'cubic');
figure(1);
meshz(xi,yi,zi);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(2),contour(xi,yi,zi,[-5 -5],'b');%contour两种形式1.contour(xi,yi,zi,[k,k])指找出zi中为k的等高线(三维等高线图为二维)，这里指水深为-5的等高线2.contour(xi,yi,n)指画出n条等高线
grid;
hold on;
plot(x,y,'+');
xlabel('X'),ylabel('Y');

拟合问题(一般为2维)

• 小样本预测
• 拟合求导

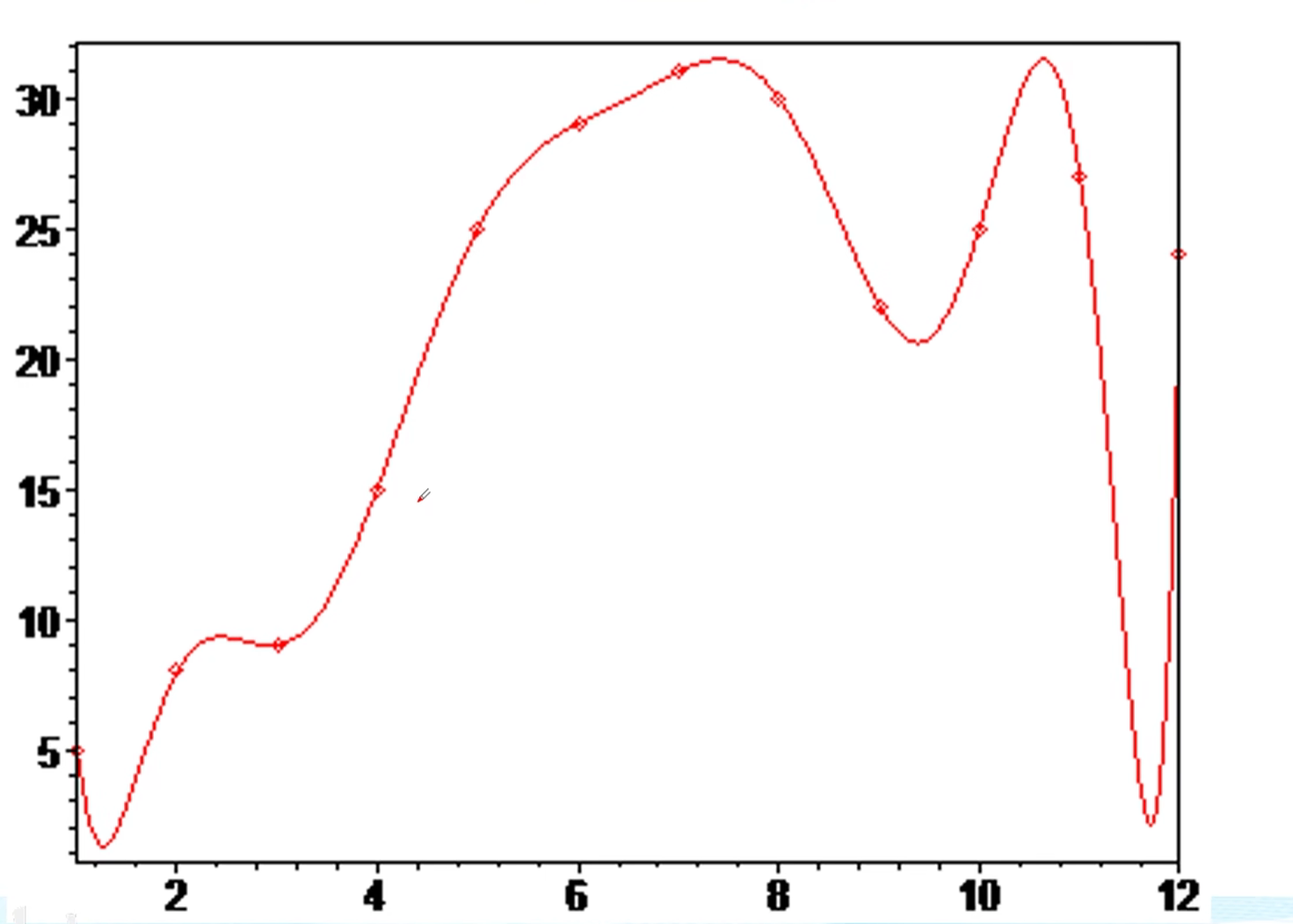
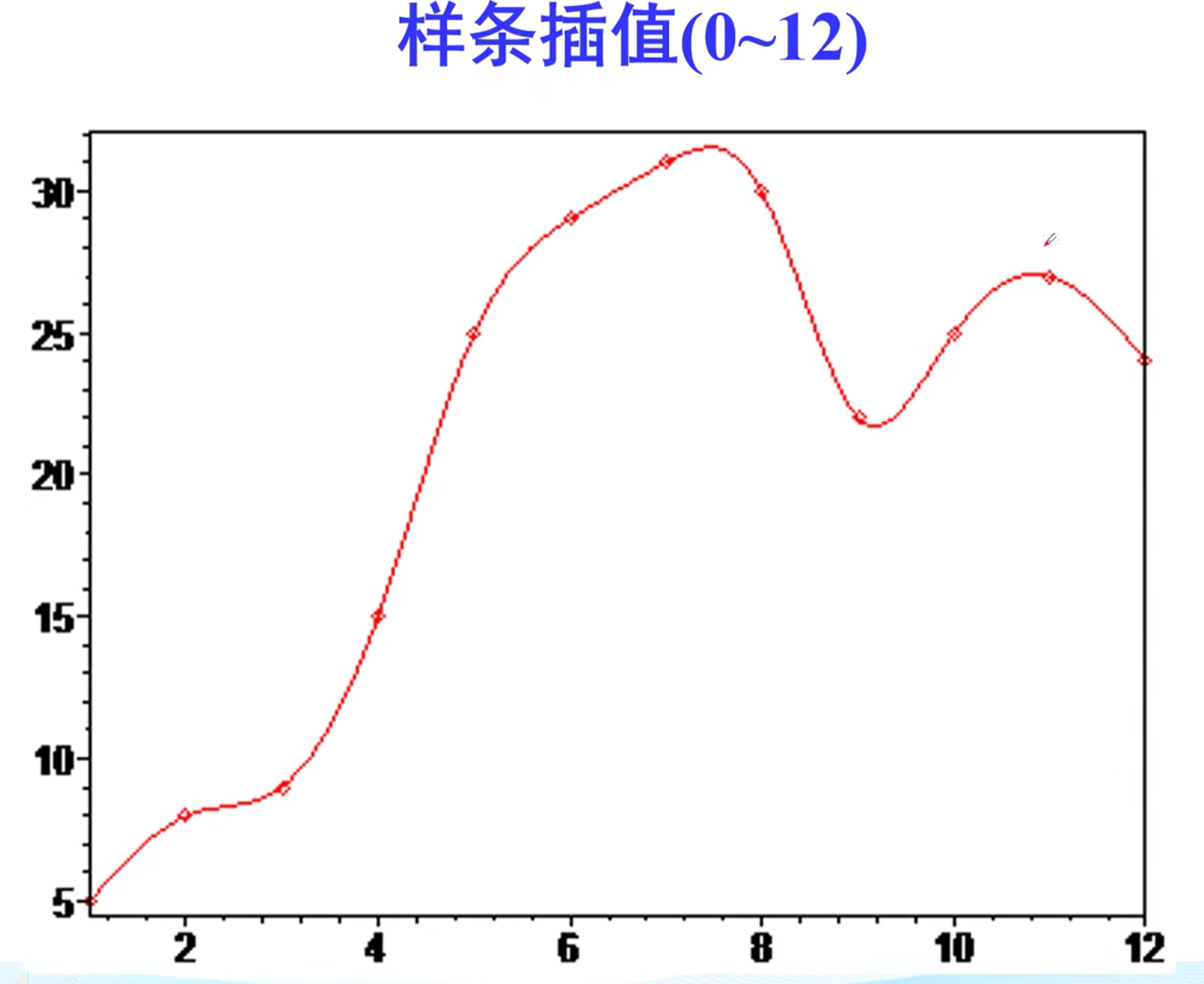
例题1.1从1点到12点每隔一个小时测量一次温度，测得的温度依次为:5,8,9,15,25,29,31,30,22,25,27

1.每隔1/10小时的温度值，并做出温度变化图形(插值法，这里就不写解答了)

2.推测t=13.5时的温度(拟合)

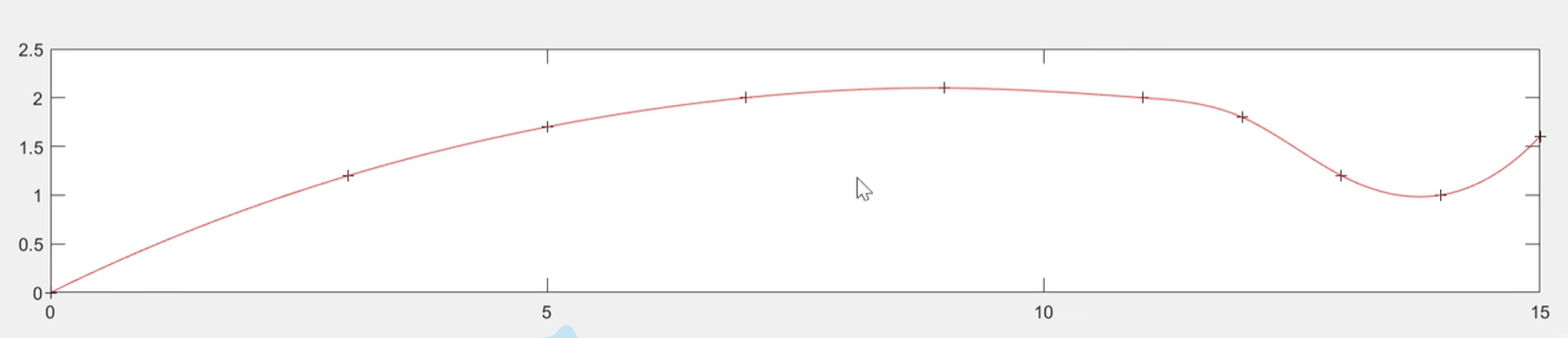
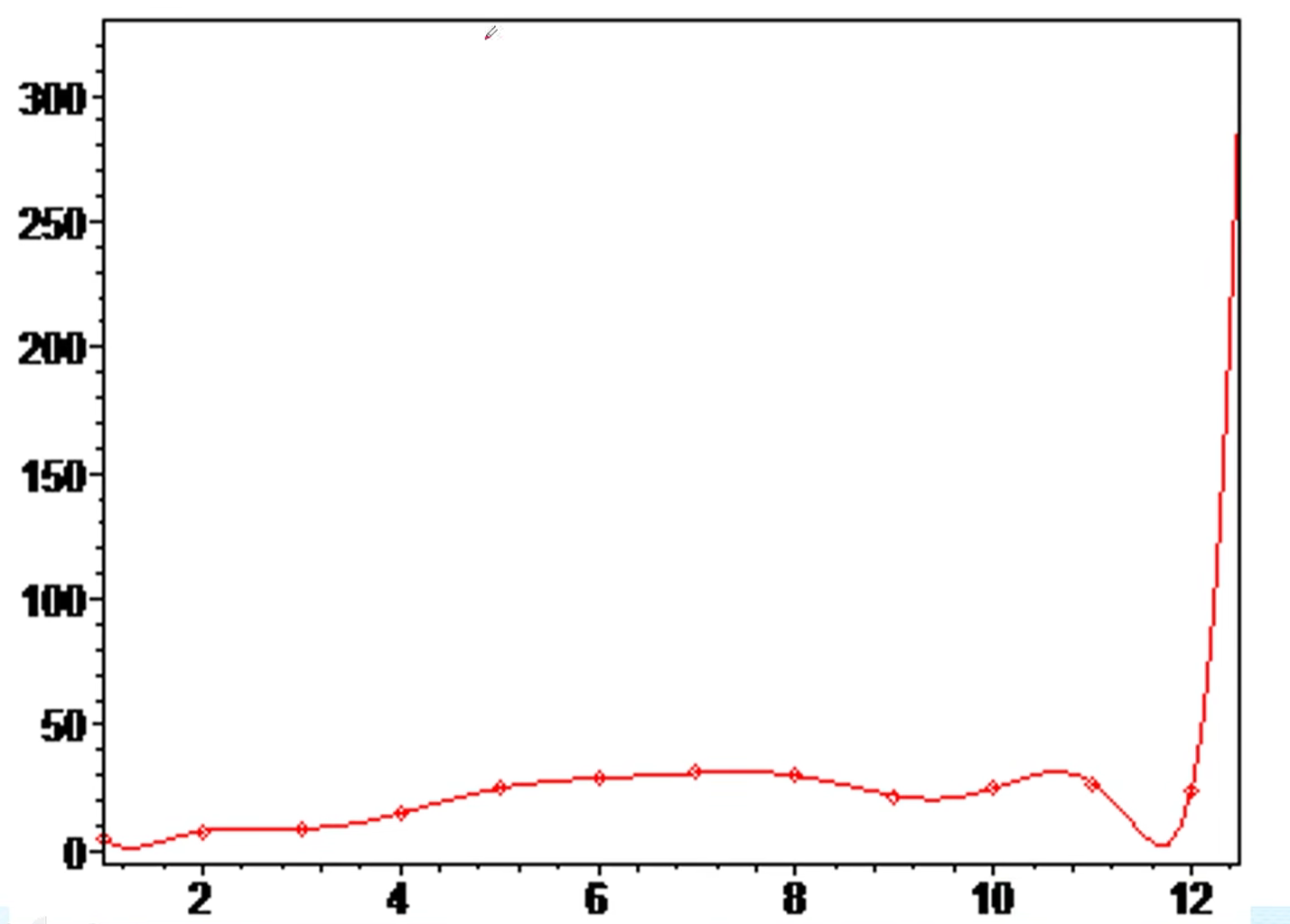
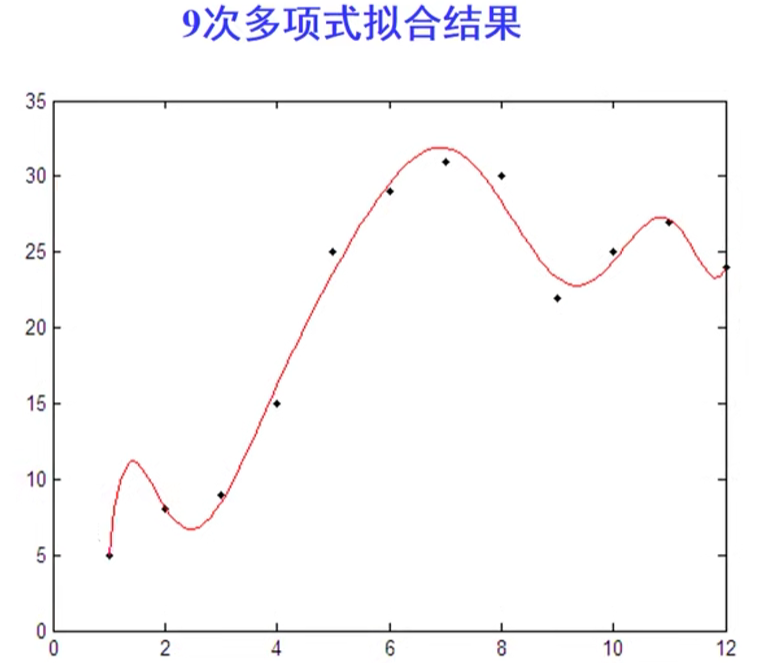
高次插值出现了Runge现象，外推t>12时的数据出现了巨大误差

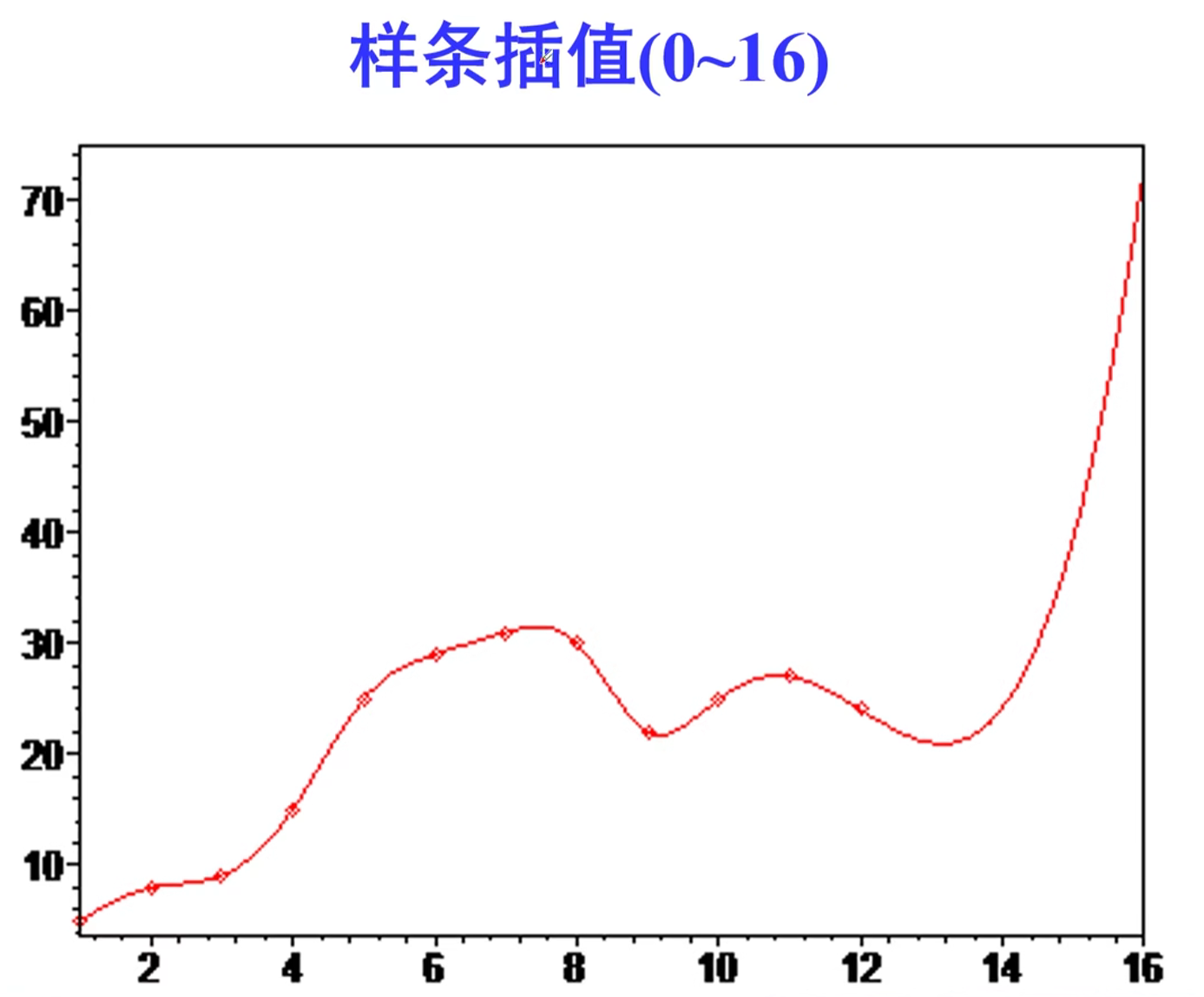
样条插值的第一个图表明样条插值可以很好地解决第一个问题，但第二个图示显示，用样条插值外推t>12时数据也会产生较大误差

拟合问题与插值问题的区别在于：

• 插值函数过已知点，而拟合函数不一定过已知点
• 插值主要用于求函数值，而拟合的主要目的是求函数关系，从而进行预测等下一步的分析

线性拟合中参数的计算可采用最小二乘法，而非线性拟合参数的计算则要用Gauss-Newton迭代法

matlab拟合(线性)

• 多项式拟合:$[a,S]=polyfit(x,y,n)$,其中x和y是被拟合数据的自变量和因变量，n为拟合多项式的系数例如:$a_1+a_2x^2+a_3x^3+a_4x^4$中系数就是4，a为拟合多项式系数构成的向量，S为分析拟合效果所需要的指标(可省略)

x=1:12;
y=[5,8,9,15,25,29,31,30,22,25,27,24];
a=polyfit(x,y,9)%插值才会出现Runge现象，现在是拟合，不会产生，9是自定义的
xp=1:0.1:12;
yp=ployval(a,xp);%y=polyval(p,x)计算多项式p在x的每个点处的值，参数p是长度为n+1的向量，其元素是n次多项式的系数
plot(x,y,'k',xp,yp,'r');

matlab(非线性拟合)

• 命令格式为:$[b,r]=ployfit(x,y,fun,b0,option)$x,y为已知点坐标fun指拟合函数，b0为拟合参数的初始迭代值，option为拟合选项，b为拟合参数，r为拟合残差
  • 非线性函数需要提前把数据点展开
  • 找近似的函数关系
  • 从近似的函数关系(fun)找未知数和初值个数(x,b)例如:$e^{-b_1x}+b_2$其中未知数就是x，初值个数为2个(b1,b2),b1和b2可以随意赋值,fun的格式就为@(x,b)，@为定义一个参数，有两个参数x和b

代码1.2(其中的函数关系为：$b_1t^{\frac{-t}{b_2}}+b_3t^{\frac{-t}{b_4}}+b_5,需要提前找到函数关系$)

x=1:16;
y=[4.00 6.40 8.00 8.80 9.22 9.50 9.70 9.86 10.00 10.20 10.30 10.42 10.50 10.55 10.58 10.60];
y1=@(b,t)b(1)*exp(-t/b(2))+b(3)*exp(-t/b(4))+b(5);
b0=[-1 1 -1 1 1];
a=polfit(x,y,y1,b0)
xp=1:0.1:16;%待拟合坐标
yp=y1(a,xp);
plot(x,y,'k',xp,yp,'r');

matlab拟合可用工具：cftool

• RMSE剩余标准差误差
• SSE平方和误差
• R-square相关系数